统计热力学 Statistic Thermodynamics
约 1855 个字 4 张图片 预计阅读时间 6 分钟
参考:Blundell, S. J., & Blundell, K. M. (2018). 热物理概念:热力学与统计物理学 ( 第 2 版 ). 许均华, 喇文, 刘志翔, 刘成 ( 译 ). 科学出版社 .
1. 能量均分
1.1 能均分定理
在很多地方我们都可以看见能量的表达式是以平方项的形式出现的,比如 \(E_k = \frac12 mv^2\),\(E_p = \frac12 kx^2\),这里我们不妨假设一个势阱可以用平方项表示:
\[ E = ax^2 \]
现在我们假设变量 \(x\) 可以等概率的在无穷的长度中取值,由 Boltzmann 定理可得,系统取得特定能量 \(\alpha x^2\) 的概率为(分母用于归一化):
\[ P(x) = \frac{e^{-\beta\alpha x^2}}{\sum_ne^{-\beta\alpha x^2}} = \frac{e^{-\beta\alpha x^2}}{\int_{-\infty}^{\infty}e^{-\beta\alpha x^2} \dd x} \]
则利用高斯矩公式,平均能量 \(\left< E \right>\) 可表示为:
\[ \begin{aligned} \left< E \right> = \int_{-\infty}^{\infty} EP(x)dx &= \frac{\int_{-\infty}^{\infty} \alpha x^2e^{-\beta\alpha x^2}\dd x}{\int_{-\infty}^{\infty}e^{-\beta\alpha x^2} \dd x} \\ &= \frac{\sqrt{\pi}/2\sqrt{\beta^3\alpha^3}}{\sqrt{\pi}/\sqrt{\beta\alpha}} \\ &= \frac1{2\beta} = \frac12 kT \end{aligned} \]
这意味着对于一个存在多个平方项能量的系统而言 :
\[ E = \sum_n a_ix_i^2 \]
其总能量:
\[ \begin{aligned} \left< E_n \right> &= \int_{-\infty}^{\infty}...\int_{-\infty}^{\infty}EP(x_1,...,x_n) \dd x_1 ... \dd x_n \\ &= \int_{-\infty}^{\infty}...\int_{-\infty}^{\infty}(\sum_n \alpha_i x_i^2)P(x_1,...,x_n) \dd x_1 ... \dd x_n \\ &= \sum_n\frac{\int_{-\infty}^{\infty}...\int_{-\infty}^{\infty}(\alpha_i x_i^2)e^{-\beta(\sum_n \alpha_i x_i^2)} \dd x_1 ... \dd x_n}{\int_{-\infty}^{\infty}...\int_{-\infty}^{\infty}e^{-\beta(\sum_n \alpha_i x_i^2)} \dd x_1 ... \dd x_n} \\ &= \sum_n\frac{\int_{-\infty}^{\infty}(\alpha_i x_i^2)e^{-\beta\alpha_i} \dd x_i}{\int_{-\infty}^{\infty}e^{-\beta\alpha_i} \dd x_i} = \frac n2 kT \end{aligned} \]
倒数第二步中,分子中每一个非 \(x_i\) 项均可与分母约去。
定义系统每一个平方能量项称作系统的一个自由度(degree of freedom),即对总能量而言,每一个自由度贡献 \(\frac 12 kT\) 的能量,这被称为能均分定理(equipartition theorem)。
注意
能均分定理的特殊之处是它所导出的能量与系统大小无关。作为例子,我们考虑一个室温下的弹簧振子:
\[ E = E_p + E_k = \frac12 kx^2 + \frac12 mv^2 = kT = \pu{0.025 eV} = \pu{2.4 kJ/mol} \]
这种能量对于一个宏观弹簧一点用都没有,但是对于原子(化学键可视作一个弹簧)来说已经是非常巨大的能量了。
拓展
借此还可以求出广义量 \(x\) 的平方的均值:
\[ \begin{aligned} \left< x_i^2 \right> = \left< E_i \right>/\alpha_i = \frac{kT}{2\alpha_i} \end{aligned} \]
如果这个量是三个方向上的动量,我们即可推导出气体的均方根速率\(\sqrt{\left< x^2 \right>} = \sqrt{\frac{3kT}{m}}\),这与宏观推导一致。
1.2 一般分子的能量和热容
对于一个一般分子来说,考虑平动和转动:
\[ E_{平动,i} = \frac12 mv_i^2 ,\quad E_{转动,i} = \frac 12 I\omega_i^2 = \frac12 \frac{L_i^2}{I} \]
均为平方能量项,因此对于每一个方向上的分能量都可以用 \(\frac12 kT\) 表示。
对于三维分子而言,平动包括 \(x,y,z\) 三个方向,于是:
\[ \left< E_{平动} \right> = \left< \frac 12 m (v_x^2 + v_y^2 + v_z^2) \right> = \frac32 kT \]
这和从宏观气体进行推导得到的结论相同。
对于振动来说考虑起来比较困难,我们不妨从双原子分子开始考虑吧:
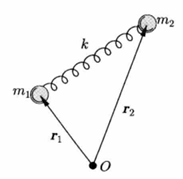
当分子开始振动时,除了考虑整体的平动能外,还需考虑相对运动(Konig 定理):
\[ E = \frac12 m(v_x^2 + v_y^2 + v_z^2) + \frac12(\frac{L_1^2}{I_1}+\frac{L_2^2}{I_2}) + \frac 12 \mu(\dot{\vec{r_1}} - \dot{\vec{r_2}}) + \frac12 k(|\vec{r_1} - \vec{r_2}| - l_0)^2 \]
按照上面的理论,我们只关心有几个平方项能量,因此:
\[ \left< E \right> = \frac72 kT \]
一般我们认为系统微观的平均能量为系统的内能(\(\left< E \right> = U\)),于是通过对能量项的求导,对于自由度为 \(f\) 的体系:
\[ C_v = N_A \dv{U}{T} =\frac f2 R,\quad C_p = (\frac f2 +1) R \]
当然,对于单原子分子而言,只存在平动自由度,因此 \(f=3\);而对于双原子分子,其一定在沿键轴方向没有转动自由度,如果算上所有的自由度则 \(f=7\)。
但是并不是所有的自由度在所有的温度下都会体现。通常情况下(室温附近),双原子气体只会体现平动和转动自由度,而振动自由度只有在极高温下才会解冻。当温度极低时,甚至转动自由度都会被冻结:
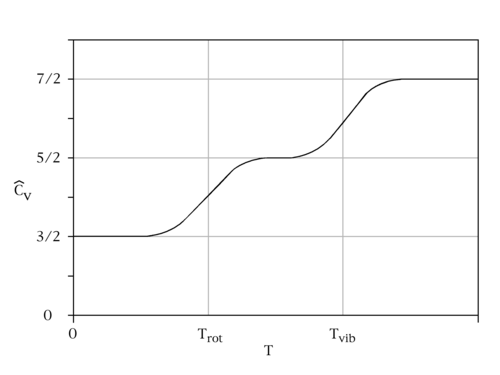
以 \(\ce{CO}\) 作为例子,\(T_{rot} \approx \pu{2.8K}\),\(T_{vib} \approx \pu{3103K}\)。对于含弱键的分子比如 \(\ce{I2}\),\(T_{vib} \approx \pu{308K}\)。事实上这一变换并不是突变,而是平滑的。
究其原因,我们知道能量是量子化的。以振动来说,其能量由 \(E = (n+\frac12)\hbar\omega\) 给出,当热能 \(kT\) 远小于能级差 \(\hbar\omega\) 时,振动能级就不可能被激发。而当它们具有大致相同的数量级时,能量的量子化就不可能被忽视,这意味着之前所做的“\(x\) 为连续量”的假设不奏效了。所以,只有当 \(kT\) 远大于能级差时,能均分定理的近似才相对较好,换句话说就是能均分定理仅在相对高温下有效。
总结
| 气体类型 | 自由度 | \(f\) | \(C_v\) | \(C_p\) | \(\gamma\) |
| 单原子气体 | 平动 | 3 | \(\frac 32 R\) | \(\frac 52 R\) | \(\frac 53\) |
| 双原子气体(极低温) | 整体平动 | 3 | \(\frac 32 R\) | \(\frac 52 R\) | \(\frac 53\) |
| 双原子气体(通常) | 整体平动 + 转动 | 5 | \(\frac 52 R\) | \(\frac 72 R\) | \(\frac 75\) |
| 双原子气体(极高温) | 整体平动 + 转动 +( 相对平动 + 振动 ) | 7 | \(\frac 72 R\) | \(\frac 92 R\) | \(\frac 97\) |
对于固体而言,原子基本没有平动和转动的自由度,因此我们只考虑振动自由度。一种近似方式是将原子视作前后左右上下连接一根弹簧:
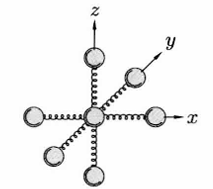
如果固体内有 \(N\) 个原子,则就有 \(3N\) 根弹簧,由于一根弹簧贡献 \(kT\) 的能量,则可得固体的平均能量和热容:
\[ \left< E \right> = 3NkT, \quad C_v = 3R \]
这就是Dulong-Petit 定律。
1.3 简谐近似
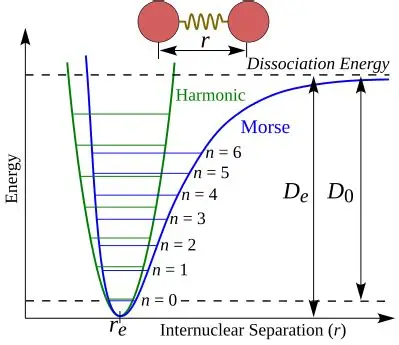
正如我们前面所讨论的,能量都是基于平方项讨论的,然而事实却没这么简单捏。如键振动势能通常用 Morse 函数表示:
\[ V(r) = -D_e+D_e\left(1-e^{-a(r-r_e)^2}\right)^2 \]
这时候我们就需要引入简谐近似(Harmonic Approximation),即将势能面近似看作是一个平方项势能(即看作是简谐的):
我们可以用泰勒展开导出。在极值点处作泰勒展开:
\[ V(x) = V(z_0) + \frac12 \left( \frac{\partial^2V}{\partial x^2} \right)_{x_0} (x-x_0)^2 + o((x-x_0)^2) \]
如果不是极高温的情况,我们可以忽略高阶项,进而得到前面平方项的能量。这意味着能均分定理近似还需要温度控制在可以忽略掉非简谐项的情况,幸运的是一般这对应的温度已经远超一般讨论范围了。
若考虑能量项非平方项,即为:
\[ E = \alpha|x|^k,\quad n=1,2,3,... \]
则我们有:
\[ P(x_i) = \frac{e^{\alpha\beta|x_i|^k}}{\int_{-\infty}^{\infty}e^{\alpha\beta|x|^k}\dd x} \]
\[ \begin{aligned} \left< E \right> = \int_{-\infty}^{\infty} EP(x)dx &= \frac{\int_{-\infty}^{\infty} \alpha |x|^ke^{-\beta\alpha |x|^k}\dd x}{\int_{-\infty}^{\infty}e^{-\beta\alpha |x|^k} \dd x} \end{aligned} \]



