近平衡态的热力学¶

约 4146 个字 4 张图片预计阅读时间 14 分钟

本文档遵循署名—非商业性使用—相同方式共享 4.0 协议（CC BY-NC-SA 4.0）授权

作者：凯楽斯kelesss

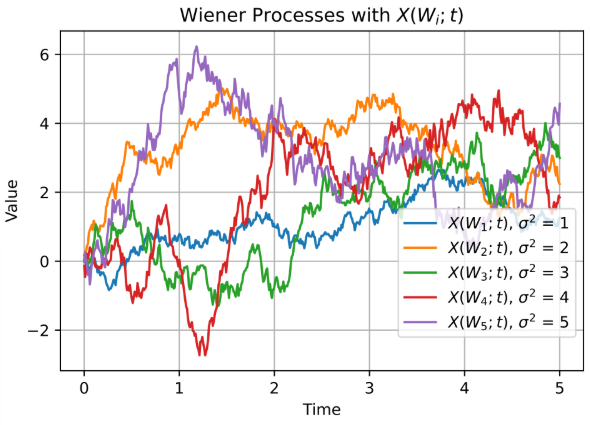
1. 布朗运动与 Langevin 方程¶

1.1 布朗运动¶

我们都知道，布朗运动（Brownian motion）指的是悬浮在介质中的微粒所做的随机运动。在数学上描述随机过程（也叫 Wiener 过程（Wiener process））通常用一个函数 \(W(t)\) 表示。

对于这个函数，你不需要了解太多的数学信息，只需要了解一些基本性质：

通常规定 \(W(0) = 0\) 。
对于任何时间 \(t\)，这个函数的增量 \((W_{t+s} - W_t)\) 都是独立的。换句话说就是维纳函数的均值为0：

\[ \ev{W(t)} = 0 \]

对于任何时间 \(t\)，这个函数的增量 \((W_{t+s} - W_t)\) 满足正态分布 \(\mathcal N(0,u)\)。
\(W(t)\) 是连续函数。

1.2 Langevin 方程¶

对于任意一个经典粒子，假设它收到一个和速度相关的阻力 \(-m\zeta u\) 和一个布朗运动相关的随机力 \(mA(t)\)，由经典的牛二定律可得：

\[ \dv{u}{t} = -\zeta u + A(t) \]

这个方程被称作朗之万方程（Langevin Equation）。

我们用常数变易法，假设 \(u = c(t)e^{-\zeta t}\) ：

\[ \begin{gathered} \dv{c}{t} e^{-\zeta t} - \zeta ce^{-\zeta t} = -\zeta u + A(t) \\ \dv{c}{t} = A(t)e^{\zeta t} \end{gathered} \]

积分得到：

\[ c = c_0 + \int_0^t A(t') e^{\zeta t'}\dd t' \]

改写成速度的形式：

\[ u = u_0e^{-\zeta t} + e^{-\zeta t}\int_0^t A(t') e^{\zeta t'}\dd t' \]

对其进行平均，而又由于第二项有随机函数，对时间的平均为0：

\[ \boxed{\ev{u} = u_0 e^{-\zeta t}} \]

现在我们考察方差。先直接对方差进行展开：

\[ \begin{aligned} \ev{(u-\ev u)^2} &= \ev{\bqty{e^{\zeta t' } \int_0^t e^{\zeta t } A(t') \dd t'}^2} \\ &= \ev{e^{2\zeta t } \int_0^t\int_0^t e^{\zeta t' } A(t') e^{\zeta t^{\prime\prime}} A(t^{\prime\prime}) \dd t'\dd t^{\prime\prime}} \\ &= e^{2\zeta t } \int_0^t\int_0^t e^{\zeta t'} e^{\zeta t^{\prime\prime}} \ev{ A(t')A(t^{\prime\prime})} \dd t'\dd t^{\prime\prime} \end{aligned} \]

这里有一个诡异的项： \(\ev{ A(t')A(t^{\prime\prime})}\) 是什么鬼？

因为随机函数对时间有平移不变性，我们不妨定义自相关函数（Autocorrelation Function）：

\[ \ev{ A(t')A(t^{\prime\prime})} = \ev{A(0)A(t^{\prime\prime} - t')} = \phi(t^{\prime\prime}-t') \]

随机力来自溶剂分子对布朗粒子的频繁碰撞。每一次碰撞都非常短暂（~ \(10^{-13}\)量级），而我们关心的布朗粒子运动的时间尺度要长得多（例如微秒或更长）。因此我们可以认为其正比于 \(\delta\) 函数：

\[ \phi(t^{\prime\prime}-t') = \Gamma\delta(t^{\prime\prime}-t') \]

于是原函数可以进一步转化：

\[ \begin{aligned} \ev{(u-\ev u)^2} &= e^{2\zeta t } \int_0^t\int_0^t e^{\zeta (t' + t^{\prime\prime})} \phi(t^{\prime\prime}-t') \dd t'\dd t^{\prime\prime} \\ &= e^{2\zeta t } \int_0^t\int_0^t e^{\zeta \tau'} \phi(\tau^{\prime\prime}) \dd (\frac{\tau' + \tau^{\prime\prime}}2 )\dd (\frac{\tau' - \tau^{\prime\prime}}2 ) \\ &= \frac 12 e^{2\zeta t } \int_0^{2t} e^{\zeta \tau'} \dd \tau' \int_{-t}^t \phi(\tau^{\prime\prime}) \dd \tau^{\prime\prime} \\ &= \frac{\Gamma}{2\zeta} \pqty{1-e^{-2\zeta t}} \end{aligned} \]

当 \(t \to \infty\):

\[ \ev{(u-\ev u)^2} = \frac{\Gamma}{2\zeta} \]

而我们又同时知道：

\[ \begin{aligned} \ev{(u-\ev u)^2} &= \ev{u^2} - 2\ev u^2 + \ev u^2 \\ &= \ev{u^2} - \ev{u}^2 \\ &= \ev{u^2} - (u_0 e^{-\zeta t})^2 = \ev{u^2} \end{aligned} \]

我们就得到速度平方的均值：

\[ \boxed{\ev{u^2} = \frac{\Gamma}{2\zeta}} \]

进一步地，我们知道分子动能：

\[ \frac{m\ev{u^2}}{2} = \frac32 kT \]

于是就可以得到：

\[ \boxed{\Gamma = \frac{6\zeta kT}{m}} \]

注意

这个结果是对于三维的情况。当然，对于一维的运动过程（更经常讨出发论）有：

\[ \Gamma = \frac{2\zeta kT}{m} \]

也就是：

\[ \ev{A(0)A(\tau)} = \frac{6\zeta kT}{m} \delta(\tau) \]

这有点奇怪，这里方程 \(\zeta\) 是一个代表“环境阻力”的量，但是我们推导出来却是一个常数，也就是物体运动不改变环境，这和现实世界的认知是不同的。因此我们需要对 Langevin 方程进行修正。

我们认为环境是“有记忆的”，用积分修正阻力项，就可以得到广义朗之万方程（generalized Langevin equations）：

\[ \dv{u}{t} = \int_{-\infty}^t -\zeta(t-t') u \dd t' + A(t) \]

另外，我们还可以求得：

\[ \ev{u(t)u(0)} = \frac{kT}{m}e^{\zeta|t|} \]

1.3 扩散效应¶

考察粒子运动的距离：

\[ \begin{aligned} r(t) - r_0 &= \int_0^t u(t') \dd t' \\ r - r_0 &= \int_0^t \bqty{u_0e^{-\zeta t'} + e^{-\zeta t'} \int_0^{t'}e^{\zeta t^{\prime\prime}} A(t^{\prime\prime}) \dd t^{\prime\prime} }dt' \\ &= \frac{1}{\zeta}u_0(1-e^{-\zeta t}) + \int_0^t\int_0^{t'} e^{-\zeta t'}e^{\zeta t^{\prime\prime}}A(t'') \dd{t''}\dd t' \\ \ev{r-r_0} &= \frac{1}{\zeta}u_0(1-e^{-\zeta t}) \end{aligned} \]

同样的，我们对于距离取平方的平均（这被称为均方位移（Mean Squared Displacement, MSD））：

\[ \begin{aligned} \ev{(r-r_0)^2} &= \ev{\pqty{\frac{1}{\zeta}u_0(1-e^{-\zeta t}) + \int_0^te^{-\zeta t'}\dd t'\int_0^{t'} e^{\zeta t^{\prime\prime}}A(t'') \dd{t''}}^2 } \end{aligned} \]

我们先处理最后一项积分:

\[ \begin{aligned} &\quad \int_0^te^{-\zeta t'}\dd t'\int_0^{t'} e^{\zeta t^{\prime\prime}}A(t'') \dd{t''} \\ &= -\frac{1}{\zeta}\bqty{e^{-\zeta t'}\eval{\int_0^{t'} e^{\zeta t^{\prime\prime}}A(t'') \dd{t''}}_0^t - \int_0^t e^{-\zeta t'} \dd(\int_0^{t'} e^{\zeta t^{\prime\prime}}A(t'') \dd{t''})} \\ &= -\frac{1}{\zeta}\bqty{e^{-\zeta t}\int_0^{t} e^{\zeta t^{\prime\prime}}A(t'') \dd{t''} - \int_0^t A(t') \dd{t'}} \\ &= \frac{1}{\zeta}\bqty{\int_0^t \pqty{A(t') - A(t')e^{\zeta(t'-t)}}\dd t'} \\ &= \frac{1}{\zeta}\bqty{\int_0^t \pqty{1 - e^{\zeta(t'-t)}}A(t')\dd t'} \end{aligned} \]

带回到原式：

\[ \begin{aligned} &\quad\ev{(r-r_0)^2} \\ &= \pqty{\frac{1}{\zeta}u_0(1-e^{-\zeta t})}^2 + 0\\ &\quad + \frac1{\zeta^2}\int_0^t\int_0^t (1-e^{\zeta (t'-t)})(1- e^{\zeta (t^{\prime\prime}-t)}) \ev{ A(t')A(t^{\prime\prime})} \dd t'\dd t^{\prime\prime}\\ \end{aligned} \]

最后一项有点抽象，我们把它拆开：

\[ \begin{aligned} &\frac1{\zeta^2}\int_0^t\int_0^t (1-e^{\zeta (t'-t)})(1- e^{\zeta (t''-t)}) \ev{ A(t')A(t'')} \dd t'\dd t'' \\ &= \frac1{\zeta^2}\int_0^t\int_0^t\frac{6\zeta kT}{m} \delta(t'' - t')(1-e^{\zeta (t'-t)} - e^{\zeta (t''-t)} + e^{\zeta (t'+t'')} e^{-2\zeta t}) \dd t'\dd t''\\ &= \frac{6 kT}{m\zeta}\int_0^t (1-2e^{\zeta (t'-t)} + e^{2\zeta (t'- t)}) \dd t' \\ &= \frac{6 kT}{m\zeta}(t-\frac2\zeta(1- e^{-\zeta t}) + \frac1{2\zeta}(1- e^{-2\zeta t})) \\ &= \frac{3 kT}{m\zeta^2}(2\zeta t - 3 + 4e^{-\zeta t} - e^{-2\zeta t}) \end{aligned} \]

我们定义扩散系数（diffusion coefficient）：

\[ \boxed{D = \frac{kT}{m\zeta}} \]

当 \(t \to \infty\)时：

\[ \begin{aligned} \boxed{\ev{(r-r_0)^2} = \frac{u_0^2}{\zeta^2} + 6Dt - \frac{9D}{\zeta} \approx 6Dt} \end{aligned} \]

这也就是说，移动距离平方和时间成正比。

注意

这个结果同样是对于三维的情况。对于一维的运动过程有：

\[ \ev{(r-r_0)^2} \approx 2Dt \]

而当 \(t \to 0\) 时，展开后面几项（对于第二项只需展开到二阶，因为第一项已经由二阶项主导）：

\[ \begin{aligned} \ev{(r-r_0)^2} &= u_0^2\pqty{\frac{1-1+\zeta t+o(t^2)}{\zeta}}^2 \\ &\quad +\frac{3 kT}{m\zeta^2}(2\zeta t - 3 + 4(1-\zeta t + \frac{\zeta^2}{2}t^2) - (1-2\zeta t + 2\zeta^2t^2))\\ &= u_0^2t^2 \end{aligned} \]

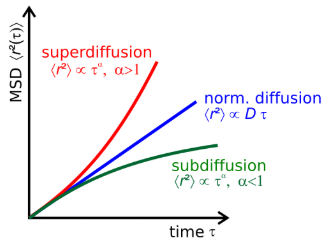
这意味着对于有初速度的典型粒子，前一段时间应观测到超扩散（superdiffusion，即MSD和超过1次的时间成正比），后一段时间观测到典型的布朗运动。

我们也可以用速度描述MSD：

\[ \begin{aligned} \ev{(r-r_0)^2} &= \ev{\int_0^t u(t')\dd t' \int_0^t u(t'')\dd t''} \\ &= \int_0^t\int_0^t \ev{u(t')u(t'')} \dd t' \dd t'' \end{aligned} \]

这一关系被称为速度关联函数（velocity-velocity correlation function）。

\[ \begin{aligned} \ev{(r-r_0)^2} &= \int_0^t\int_0^t \ev{u(0)u(t''-t')} \dd t' \dd t'' \\ &= \int_{0}^{t-\tau}\dd t'\int_{-t}^t \ev{u(0)u(\tau)} \dd \tau \\ &= 2t\int_0^{t} (1-\frac{\tau}{t})\ev{u(0)u(\tau)} \dd \tau \end{aligned} \]

当 \(t \to \infty\)：

\[ \ev{(r-r_0)^2} = 2t\int_0^\infty\ev{u(0)u(\tau)} \dd \tau = 6Dt \]

这就得到了扩散系数的表达式：

\[ \boxed{D = \frac{1}{3}\int_0^\infty \ev{u(0)u(\tau)} \dd \tau} \]

这一关系被称为 Green-Kubo 关系（Green–Kubo relations）。这意味着扩散能力取决于速度“记忆”多长时间：

若速度相关衰减很快（短记忆），积分有限，扩散系数有限。
若相关衰减慢（长尾），扩散系数可能发散（反常扩散）。

2. 扩散方程¶

2.1 扩散定律¶

假设有一个特定的力作用在粒子上：

\[ m\dv{u}{t} = F - \eta u + A(t) \]

我们知道某一方向上的扩散通量（flux）\(j_D\)，由 Fick 第一定律知道，扩散通量和密度梯度成正比：

\[ j_D = -D_x\pdv{\rho}{x} \]

其中 \(\rho\) 是密度分布函数。为了简便，我们先把 \(D_x\) 当作常量。

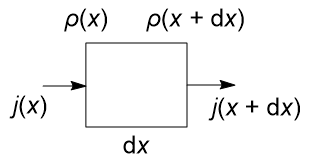
对于一段距离内的通量，我们有：

\[ \begin{aligned} \pdv{\rho}{t}\dd x \dd y \dd z &= j(x)\dd y \dd z - j(x+\dd x)\dd y \dd z \\ \pdv{\rho}{t}\dd x &= j(x) - \pqty{j(x) + \pdv{j}{x}\dd x} \\ \pdv{\rho}{t} &= -\pdv{j}{x} \end{aligned} \]

于是在仅考虑扩散的情况下：

\[ \boxed{\pdv{\rho}{t} = D\pdv x\pqty{\pdv{\rho}{x}} = D\pdv[2]{\rho}{x}} \]

这被称为扩散方程（Diffusion Equation，或 Fick 第二扩散定律）。

当由外力作用时，考虑 \(\dd u / \dd t = 0\) 时，由于力平衡有：

\[ \ev{u} = \frac{F}{m\zeta} \]

于是可以把通量拆分成扩散通量和由外力造成的分量：

\[ j = j_F + j_D = \frac{\rho F}{m\zeta} - D\pdv{\rho}{x} \]

由扩散方程可得：

\[ \begin{aligned} \pdv{\rho}{t} &= -\pdv{j}{x}\\ &= \pdv{x}\pqty{\frac{\rho F}{m\zeta}} + D\pdv[2]{\rho}{x}\\ &= \pdv{x}\pqty{\frac{\rho}{m\zeta}\pdv{V}{x}} + \frac{kT}{m\zeta}\pdv[2]{\rho}{x} \end{aligned} \]

于是当 \(t \to \infty\) 时，可认为密度梯度趋向平稳（\(\displaystyle \pdv{\rho}{t}=0\)），积分一次可以得到：

\[ \rho\pdv{V}{x} + kT\pdv{\rho}{x} = C \]

在无边界流时，可认为 \(C = 0\) 。解微分方程可得：

\[ \rho_{eq} = \rho_0 e^{-V(x)/k_BT} \]

这就是 Boltzmann 分布。

2.2 扩散方程的调和分析¶

我们考虑 Langevin 方程：

\[ \dv{u}{t} = -\zeta u + A(t) \]

我们现在需要知道其在光谱的显示。此时，对白噪声 \(A(t)\) 作连续傅里叶变换：

\[ a(\omega) = \frac{1}{2\pi}\int_{-\infty}^{\infty} A(t)e^{i\omega t} \dd t \]

\[ A(t) = \int_{-\infty}^{\infty} a(\omega)e^{i\omega t} \dd\omega \]

作为例子，当 \(\omega=0\) 时：

\[ a(0) = \frac1{2\pi}\int_{-\infty}^{\infty}A(t)\dd t = \frac{T\ev{A}}{2\pi} \]

注意这里我们积分的时候，由于出现了无穷，应当认为这是一个很长的时间，即可以认为是在区间 \([-T/2, T/2]\) 内积分。

对于光谱来说，我们关心每一个频率的功率谱密度 \(I(\omega)\)，一般认为这是傅里叶系数的平方的均值：

\[ \begin{aligned} |a(\omega)|^2 &= \frac{1}{4\pi^2}\bqty{\int_{-\infty}^{\infty} A(t)e^{i\omega t} \dd t}^*\bqty{\int_{-\infty}^{\infty} A(t)e^{i\omega t} \dd t}\\ &= \frac{1}{4\pi^2}\int_{-\infty}^{\infty}\int_{-\infty}^{\infty} A(t)A(t'')e^{i\omega (t'' - t')} \dd t' \dd t'' \end{aligned} \]

\[ I'(\omega) = \ev{|a(\omega)|^2} = \frac{1}{4\pi^2}\int_{-\infty}^{\infty}\int_{-\infty}^{\infty} \ev{A(t)A(t'')}e^{i\omega (t'' - t')} \dd t' \dd t'' \]

我们进行变量替换 \(t'' = t' + \tau\) ：

\[ \begin{aligned} I'(\omega) &= \frac{1}{{4\pi^2}}\int_{-\infty}^\infty\int_{-\infty}^\infty \ev{A(\tau)A(0)} e^{i\omega \tau} d\tau dt' \\ &= \frac{T}{4\pi^2}\int_{-\infty}^\infty \phi(\tau)e^{i\omega \tau}\dd \tau \end{aligned} \]

之后对时间作平均：

\[ I(\omega) = \frac{2I'(\omega)}{T} = \frac{1}{2\pi}\int_{-\infty}^\infty \phi(\tau)e^{i\omega \tau}\dd \tau = \mathcal F(\phi(t)) \]

这被称为 Wiener-Khinchin 定理（Wiener–Khinchin theorem），即白噪声的功率谱密度是自相关函数的傅里叶变换，换句话说就是对 \(\delta\) 函数作傅里叶变换，也就是常数。

\[ I(\omega) = \frac{1}{2\pi}\int_{-\infty}^\infty \Gamma \delta(\tau) e^{i\omega \tau}\dd \tau = \frac{\Gamma}{2\pi} \]

对于 Langevin 方程，我们也作傅里叶变换：

\[ \begin{aligned} \mathcal F(\dv{u}{t}) &= \frac{1}{2\pi} \int_{-\infty}^\infty \dv{u}{t} e^{-i\omega t} \dd t \\ &= \eval{\frac{1}{2\pi} u e^{-i\omega t}}_{-\infty}^\infty - \frac{1}{2\pi} \int_{-\infty}^{\infty}u(-i\omega)e^{-i\omega t} \dd t \\ &= i\omega\tilde{u} \\ &= \mathcal F[\zeta u + A(t)] = \zeta\tilde u + a(\omega) \end{aligned} \]

解方程可以得到：

\[ \tilde u(\omega) = \frac{a(\omega)}{i\omega + \zeta} \]

取平方的均值，因为我们知道 \(a(\omega)\) 的均值是常数 \(a\)：

\[ \ev{\abs{\tilde u(\omega)}^2 }= \frac{a^2}{\omega^2 + \zeta^2} \]

注意

有的文献也会写成：

\[ \abs{\tilde u(\omega)}^2= \frac{a^2}{\omega^2 + \zeta^2} \]

这里可以认为 \(\abs{\tilde u(\omega)}^2\) 已经在长时间观测到的频谱层面了，所以可以直接写 \(a\) 。

之后我们傅里叶变换回去：

\[ u(t) = \int \frac{a(\omega)}{i\omega + \zeta} e^{i\omega t}\dd \omega \]

由于我们知道自相关函数就是频率谱函数的逆傅里叶变换，我们有：

\[ \phi(t) = \ev{u(t)u(0)} = \int_{-\infty}^{\infty} \frac{a^2}{\omega^2 + \zeta^2}e^{i\omega t} \dd \omega = \frac{\pi a^2}{\zeta} e^{-\zeta\abs{t}} \]

上面这个积分可以用围道积分求得。我们又知道，平衡态的自相关函数：

\[ \ev{u(t)u(0)} = \frac{kT}{m}e^{-\zeta|t|} \]

比较系数可以得到：

\[ a^2 = \frac{\zeta kT}{\pi m} = \frac{\Gamma}{2\pi} \]

这可以与上面 Wiener-Khinchin 定理得到的结论匹配。

我们还可以对扩散方程进行傅里叶变换：

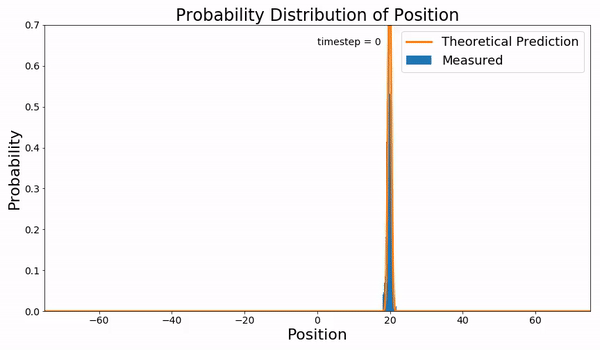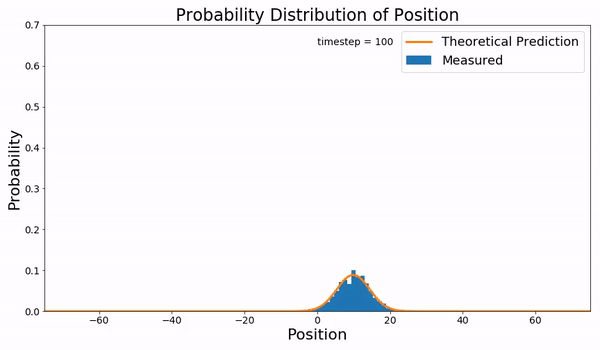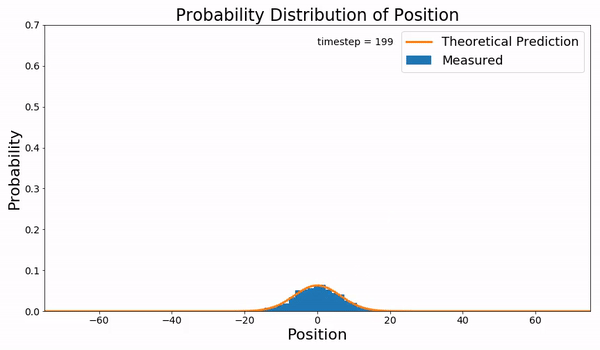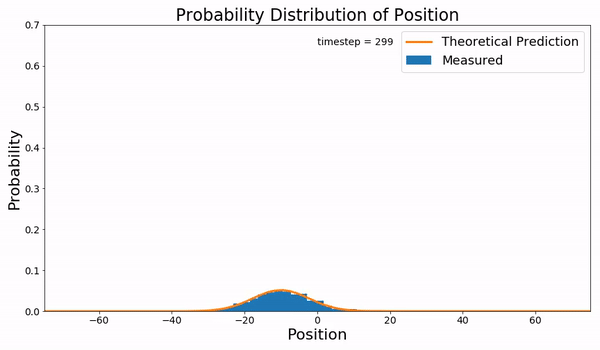
\[ \begin{aligned} \pdv{\rho}{t} &= D\pdv[2]{\rho}{x} \\ \pdv{\tilde \rho}{t} &= -D\omega^2\tilde \rho \\ \tilde \rho &= Ce^{-D\omega^2t} \\ \rho(x,t) &= \frac{C}{2\pi}\int_{-\infty}^\infty e^{i\omega x}e^{-D\omega^2 t} \dd \omega \\ \rho(x,t) &= \frac{\rho_0}{2\sqrt{\pi D t}} e^{-\frac{x^2}{4Dt}} \end{aligned} \]

这意味着扩散会使例子的峰展宽成高斯分布（一般认为初始是一个 \(\delta\) 函数，并且方差随时间增长）：

如果我们结合前面的势能 \(V\) 作用，可以同时观察到中心点向势能低点移动并展宽。

2.3 Fokker-Plank 方程¶

假设需要从前一刻的状态 \(\rho(u-\Delta u, t)\) 计算下一刻的状态 \(\rho(u, t + \Delta t)\) ，可以利用一个状态转移函数 \(\Psi(u-\Delta u; \Delta u)\) （表示当前速度是 \((u-\Delta u)\)，在 \(\Delta t\) 后变化量为 \(\Delta u\) 的概率）表示：

\[ \rho(u, t + \Delta t) = \int \rho(u-\Delta u, t) \Psi(u-\Delta u; \Delta u) \dd(\Delta u) \]

对这三个函数分别做泰勒展开，对于时间项只需要展开到一阶（因为我们要取其趋于0）：

\[ \begin{gathered} \rho(u, t + \Delta t) = \rho(u,t) + \pdv{\rho}{t} \Delta t + ...\\ \rho(u-\Delta u, t) = \rho(u,t) - \pdv{\rho}{u} \Delta u + \frac12 {\pdv[2]{\rho}{u}}(\Delta u)^2\\ \Psi(u-\Delta u; \Delta u) = \Psi(u; \Delta u) - \pdv{\Psi}{u}\Delta u + \frac12 {\pdv[2]{\Psi}{u}}(\Delta u)^2 + ... \end{gathered} \]

于是：

\[ \begin{aligned} &\rho(u,t) + \pdv{\rho}{t} \Delta t \\ &= \int_{-\infty}^{\infty} \bqty{\rho(u,t) - \pdv{\rho}{u} \Delta u + \frac12 {\pdv[2]{\rho}{u}}(\Delta u)^2 + ...} \\ &\quad\bqty{\Psi(u; \Delta u) - \pdv{\Psi}{u}\Delta u + \frac12 {\pdv[2]{\Psi}{u}}(\Delta u)^2 + ...} \dd (\Delta u ) \\ &\approx \int_{-\infty}^{\infty} \rho\Psi - \Delta u\pqty{\Psi\pdv{\rho}{u}+\rho\pdv{\Psi}{u}} + \\&\quad(\Delta u)^2 \pqty{\frac12\pdv[2]{\rho}{u}\Psi + \pdv{\rho}{u}\pdv{\Psi}{u} + \frac12 \rho \pdv[2]{\Psi}{u}} \dd(\Delta u) \end{aligned} \]

我们先来看零阶项，其中积分和密度分布函数无关：

\[ \begin{aligned} \int_{-\infty}^{\infty} \rho\Psi \dd(\Delta u) &= \rho(u,t) \int_{-\infty}^{\infty} \Psi(u;\Delta u) \dd(\Delta u) \\ &= \rho(u,t) \end{aligned} \]

这正好与左边的第一项消去。对于一阶项：

\[ \begin{aligned} \int_{-\infty}^{\infty} \pdv{\rho}{u}(\Delta u)\Psi \dd(\Delta u) &= \pdv{\rho}{u} \int_{-\infty}^{\infty} (\Delta u)\Psi(u;\Delta u) \dd(\Delta u) \\ &= \pdv{\rho}{u} \ev{\Delta u} \end{aligned} \]

\[ \begin{aligned} \int_{-\infty}^{\infty} \pdv{\Psi}{u}(\Delta u)\rho \dd(\Delta u) &= \rho(u,t) \pdv{u}\int_{-\infty}^{\infty} (\Delta u)\Psi(u;\Delta u) \dd(\Delta u) \\ &= \rho(u,t) \pdv{\ev{\Delta u}}{u} \end{aligned} \]

两个合在一起就可以得到：

\[ \pdv{\rho}{u} \ev{\Delta u} + \rho(u,t) \pdv{\ev{\Delta u}}{u} = \pdv{u}(\rho\ev{\Delta u}) \]

我们把二阶项作一样的操作，最终原方程可以变成：

\[ \boxed{\pdv{\rho}{t} \Delta t = -\pdv{u}(\rho\ev{\Delta u}) + \frac 12 \pdv[2]{u}(\rho\ev{\Delta u^2})} \]

这就是 Fokker-Plank 方程（Fokker–Planck equation）。

我们直接给出三维情况下的方程：

\[ \pdv{\rho}{t} \Delta t = -\sum_{j=1}^3\pdv{u_j}(\rho\ev{\Delta u_j}) + \frac 12 \sum_{i=1}^3\sum_{j=1}^3{\pdv[2]{}{u_i}{u_j}}(\rho\ev{\Delta u_i\Delta u_j}) \]

对于每一项，我们前面都可以求得：

\[ \begin{gathered} \ev{\Delta u_j} = u_j(e^{-\zeta\Delta t} - 1) = -\zeta u_j \Delta t \\ \ev{\Delta u_j^2} = \frac{2\zeta kT}{m}\Delta t \end{gathered} \]

假设 \(\ev{\Delta u_i\Delta u_j} = 0\)：

\[ \pdv{\rho}{t} = \zeta\bqty{\sum_{j=1}^3\pdv{u_j}(\rho u_j) + \frac{kT}{m} \sum_{j=1}^3{\pdv[2]{u_j}}\rho} \]

利用 Vlasov 方程，可以改成相空间的表示：

\[ \begin{aligned} \rho(r,u, t + \Delta t) &= \int \rho(r-\Delta r,u-\Delta u, t) \\ &\quad\quad \Psi(r-\Delta r, u-\Delta u; \Delta r, \Delta u) \dd(\Delta r)\dd(\Delta u) \end{aligned} \]

解出来得到这个结果：

\[ \pdv{\rho}{t} + \vb u\cdot \grad_\vb r \rho + \frac{\vb F_{ext}}{m} \cdot \grad_\vb u \rho = \zeta \grad_\vb u (\rho \vb u) + \frac{\zeta kT}{m}\grad_\vb u^2 \rho \]

而我们之前说过扩散方程：

\[ \pdv{\rho}{t} = D\grad_\vb{r}^2 \rho \]

这实际上是达到平衡后的结果，因为当体系达到平衡时，可以认为体系不再扩散（即关于速度的梯度均为0）。