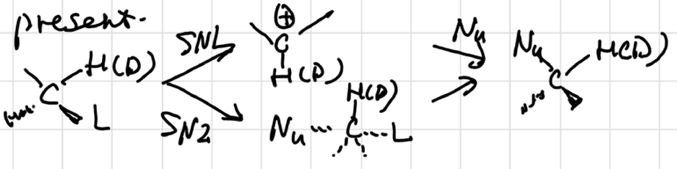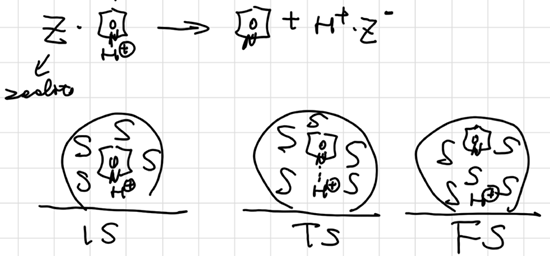Physical Chemistry II 物理化学 II 笔记
约 5633 个字 5 行代码 34 张图片 预计阅读时间 19 分钟
注意
此页面为物理化学 II 英文班的笔记,因此较为粗略。详细内容我之后会单开页面重新编写。
Chapter 1 : Chemical and Electrochemical Equilibrium
Gibbs Energy Minimum
for rxn \(A \rightleftarrows B\), def. \(\xi\) as rxn extent(mol)
so \(-\dd n_A = \dd n_B = \dd \xi\),
\[ \dd G = \mu_A \dd n_A + \mu_B \dd n_B = (\mu_A-\mu_B)\dd\xi \]
for
\[ \Delta_rG = \dv{G}{\xi} = \mu_B - \mu_A = \mu_B^{\circ} - \mu_A^{\circ} + RT\ln{\frac{p_B}{p_A}} \]
def. rxn quotient \(Q = \frac{p_B}{p_A}\)
at Eq. \(0 = \Delta_rG = \Delta_rG^{\circ} + RT\ln{K}\)
General rxns
\[ \nu_A A + \nu_B B \rightleftarrows \nu_C C + \nu_D D \]
we get:
\[ \Delta_rG = \Delta_rG^{\circ} + RTlnQ = \sum_j \nu_j \Delta_fG^{\circ}(j) + RT\ln(\prod_j a_j^{\nu_j}) \]
as \(a_j\) remains activity or fugacity
Since \(\delta _rG^{\circ}\) is defined as a single pressure, we have \((\frac{\partial K}{\partial p})_T = 0\)
for rxn \(A \rightleftarrows 2B\), \(A\) changes from \(n\) to \((1-\beta)n\)
\[ x_A = \frac{(1-\beta)n}{(1-\beta)n + 2\beta n}, x_B = \frac{2\beta n}{(1-\beta)n + 2\beta n} \]
so we have:
\[ \begin{gathered} K = \frac{p_B^2}{p_A p^{\circ}} = \frac{x_B^2}{x_A} (\frac{p}{p^{\circ}}) = \frac{4\beta^2}{1-\beta^2}(\frac{p}{p^{\circ}}) \\ \beta = \frac{1}{(1+4 p/Kp^{\circ})^{1/2}} \end{gathered} \]
as \(p\) increase, \(\beta\) decrease.
Response of equilibria to changes
as
\[ \ln{K} = -\frac{\Delta_rG^{\circ}}{RT} = -\frac{1}{R} (\frac{\partial \Delta_rG^{\circ}/T}{\partial T}) = \frac{\Delta_rH^{\circ}}{RT^2} \]
that is:
\[ \frac{\partial \ln{K}}{\partial {1/T}} = -\frac{\Delta_rH^{\circ}}{R} \]
that means: when \(\Delta_rH^{\circ} < 0\), when \(T\) decrease, \(K\) increase. Vice Versa
Equilibrium electrochemistry
for rxn \(\ce{H_2O <--> H_2 + O_2}\) we got half rxns:
Anode: \(\ce{H_2 - 2e^-<--> 2H^+}\)
Cathode: \(\ce{0.5O_2 + 2H^+ + 2e^- <--> H_2O}\)
for non-electrochemistry states:
\[ Q_1 = \frac{a(\ce{H^+})^2}{(p(\ce{H_2})/p^{\circ})}, Q_2 = \frac{a(\ce{H2O})}{(p(\ce{O_2})^{1/2}/p^{\circ})a(\ce{H^+})^2} \]
consider the Electromotive Force(EMF)
\[ \begin{aligned} -\nu EF = \Delta_rG &= \Delta_rG^{\circ} + RT\ln{Q} = \dv{W_e}{\xi}\\ E &= -\frac{\Delta_rG_m^{\circ}}{\nu F} - \frac{RT}{\nu F} \ln{Q} \end{aligned} \]
this is called Nerst Equation.
At eq: \(0 = E^{\circ} - \frac{RT}{\nu F}\ln{K}\), so
\[ \ln K = \frac{\nu FE^{\circ}}{RT} \]
Lattice gas
def. \(N\) as indistinguishable particles, \(N_0\) as indistinguishable sites
as Boltzman Entropy \(S = k_B \ln{\Omega}\), since \(\displaystyle \Omega = \frac{N_0!}{(N_0 - N)!(N)!}\)
let \(x = N/N_0\), using Stiring Approximation:
\[ S = -k_BN(x\ln{x} + (1-x)\ln{1-x}) \]
for general cases:
\[ S = -k_BN(\Sigma_n x_i\ln{x_i}) \]
Electrochemical Potential
\[ G = H - TS + zeN\varphi \]
\[ \Delta G = \Delta H - T\Delta S + \Delta(zeN)\varphi \]
so as \(\displaystyle \mu = (\frac{\Delta G}{\Delta N})_{T,p,\varphi} = (\frac{\partial g}{\partial x})_{T, p, \varphi}\), def \(g = G/N, h = H/N, S = S/N\)
For a lattice as:
\[ S' = (\frac{\partial S}{\partial x})_{T,p,\varphi} = k_B \frac{x}{1-x} \]
so:
\[ \mu = h' + k_BT\ln{\frac{x}{1-x}} + ze\varphi \]
in solution, when \(x \rightarrow 0\),
\[ \mu = \underline{h' + k_BT\ln{x}} + ze\varphi = k_BT\ln{\gamma x} + ze\varphi \]
that is called Electrochemical Potential
Standard Hydrogen Potential
define Standard Hydrogen Potential as 0 V as the Standard Hydrogen Electrode:
\[ \ce{2H^+ + 2e^- -> H_2} \quad E^\circ = \pu{0V} \]
whereas happens Pt electrode and every species are at the standard state ( 形成铂黑结构增加催化位点,促进反应快速达到平衡。)
eg: \(\ce{2H_2 + O_2 -> 2H_2O}\), \(E = \pu{1.23V}\)
so \(\ce{0.5O_2 + 2H^+ + 2e^- <--> H_2O}\), \(E = \pu{1.23V}\)
eg2: \(\ce{AgCl + e <--> Ag + Cl^-}\)
\[ \begin{aligned} E &= E_{AgCl/Ag}^{\circ} - \frac{RT}{F} ln{a(\ce{Cl^-})} + \frac{RT}{F} ln{\frac{1}{a(\ce{H^+})}} \\ &= E_{AgCl/Ag}^{\circ} - \frac{RT}{F} \ln{a(\ce{Cl^-})a(\ce{H^+})}\\ &= E_{AgCl/Ag}^{\circ} - \frac{RT}{F} \ln{b(\ce{Cl^-})b(\ce{H^+})} -\frac{RT}{F} \ln{\gamma(\ce{Cl^-})\gamma(\ce{H^+})} \end{aligned} \]
where \(b\) stands molality( 质量摩尔浓度 ), \(\gamma\) stands activity coefficient
as Debye-Huckle Formula \(\ln{\gamma} = cb^{1/2}\):
\[ E = E_{AgCl/Ag}^{\circ} - \frac{2RT}{F} \ln{b} +\frac{2RT}{F} cb^{1/2} \]
Reversible Hydrogen Electrode (RHE)
\[ E_{RHE}^{\circ} = E_{SHE} + \frac{RT}{F} \ln{a(\ce{H^+})}\\ V_{RHE}^{\circ} = V_{SHE} - \frac{RT}{F} \ln{a(\ce{H^+})} = V_{SHE} + 0.059\mathrm{pH} \]
Eg: Water Electrolysis
\[ \begin{aligned} V_{SHE} &= E^{\circ} - \frac{RT}{4F}\ln{\frac{1}{(p(\ce{O_2}/p^{\circ}))a(\ce{H^+})^4}} \\ &= E^{\circ} + \frac{RT}{F} \ln{a(\ce{H^+})} + \frac{RT}{4F} \ln{p(\ce{O_2})/p^{\circ}} \end{aligned} \]
where \(\displaystyle V_{RHE} = E^{\circ} + \frac{RT}{4F} \ln(p(\ce{O_2})/p^{\circ})\)
In real case, if we want to drive the rxn, need let \(E > E^{\circ} = 1.23 \mathrm{V}\)
Chapter 2 : Fuel Cells, Batteries and Electric Double Layer
Determining TD functions
\[ \begin{gathered} \Delta_rG^{\circ} = \Delta_rH^{\circ} - T\Delta_rS^{\circ} = -\nu FE^{\circ}\\ \frac{\dd E^{\circ}}{\dd T} = \frac{\Delta_rS^{\circ}}{\nu F} \to \Delta_rS^{\circ} = \nu F\dv{E^{\circ}}{T}\\ \Delta_rH^{\circ} = \Delta_rG^{\circ} + T\Delta_rS^{\circ} = -\nu F(E^{\circ} - T\dv{ E^{\circ}}{T}) \end{gathered} \]
Energy Efficiency
\[ \begin{gathered} \text{Fuel Cell}(EE) = \frac{\text{Electrical }E}{\text{Chemical }E}\\ \text{Electrolyzer}(EE) = \frac{\text{Chemical }E}{\text{Electrical }E} \end{gathered} \]
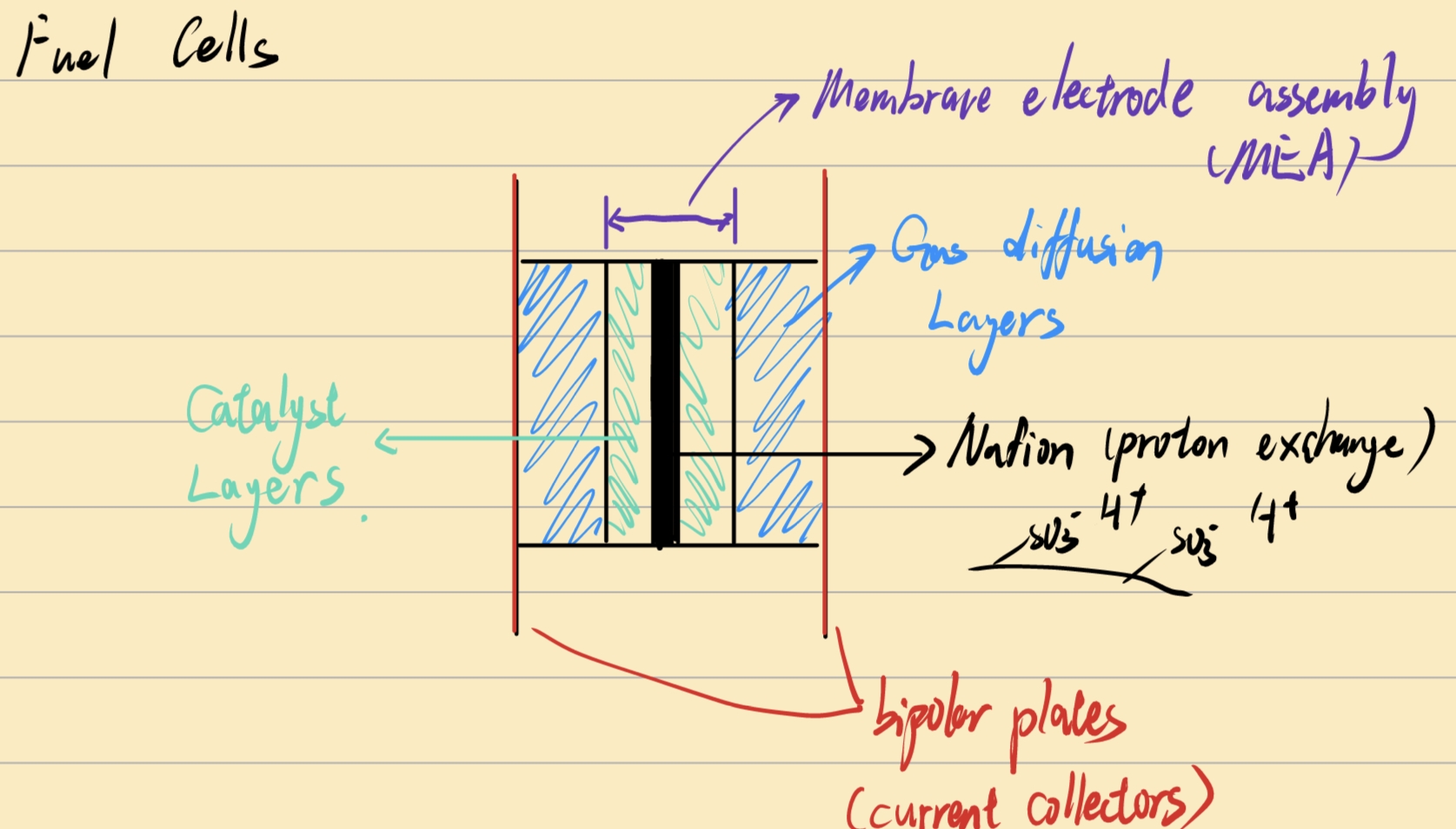
MEA: 膜电极组件
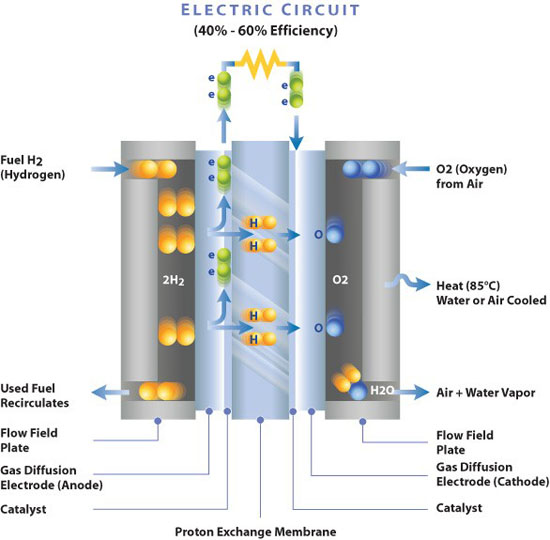
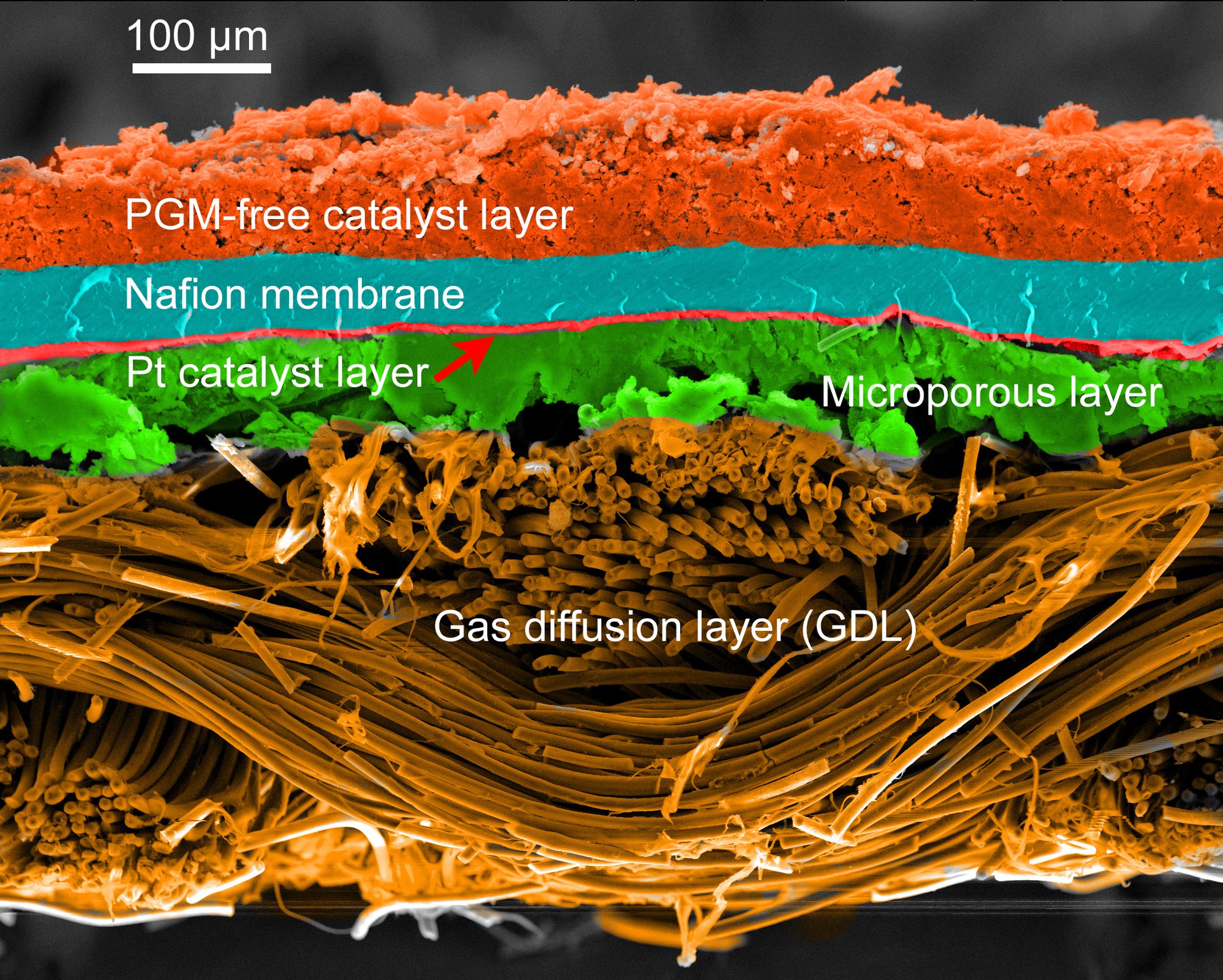
Rechargable batteries
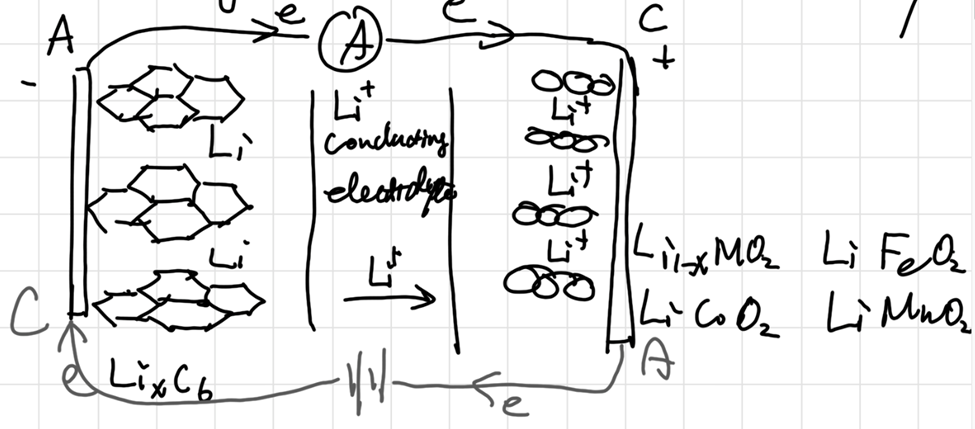
Charging Mode
- Positive Electrode: supply e-(Sluggish) Anode
- Negative Electrode: receive e-(Energetic) Cathode
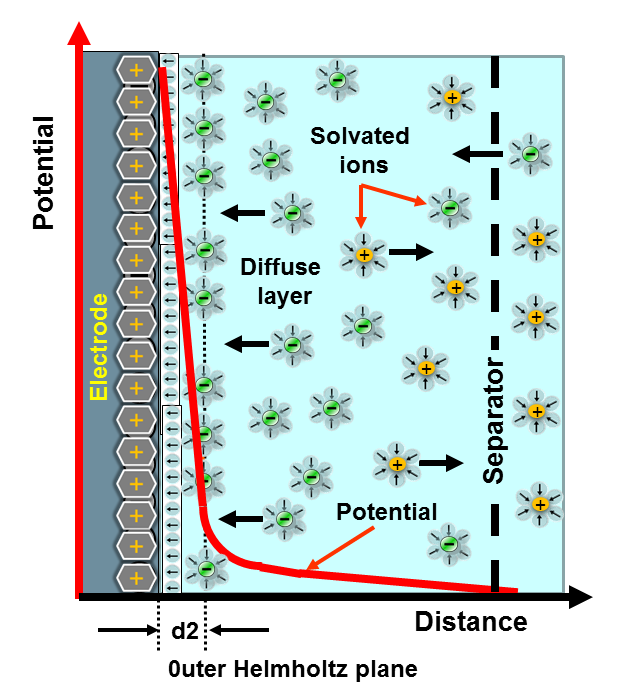
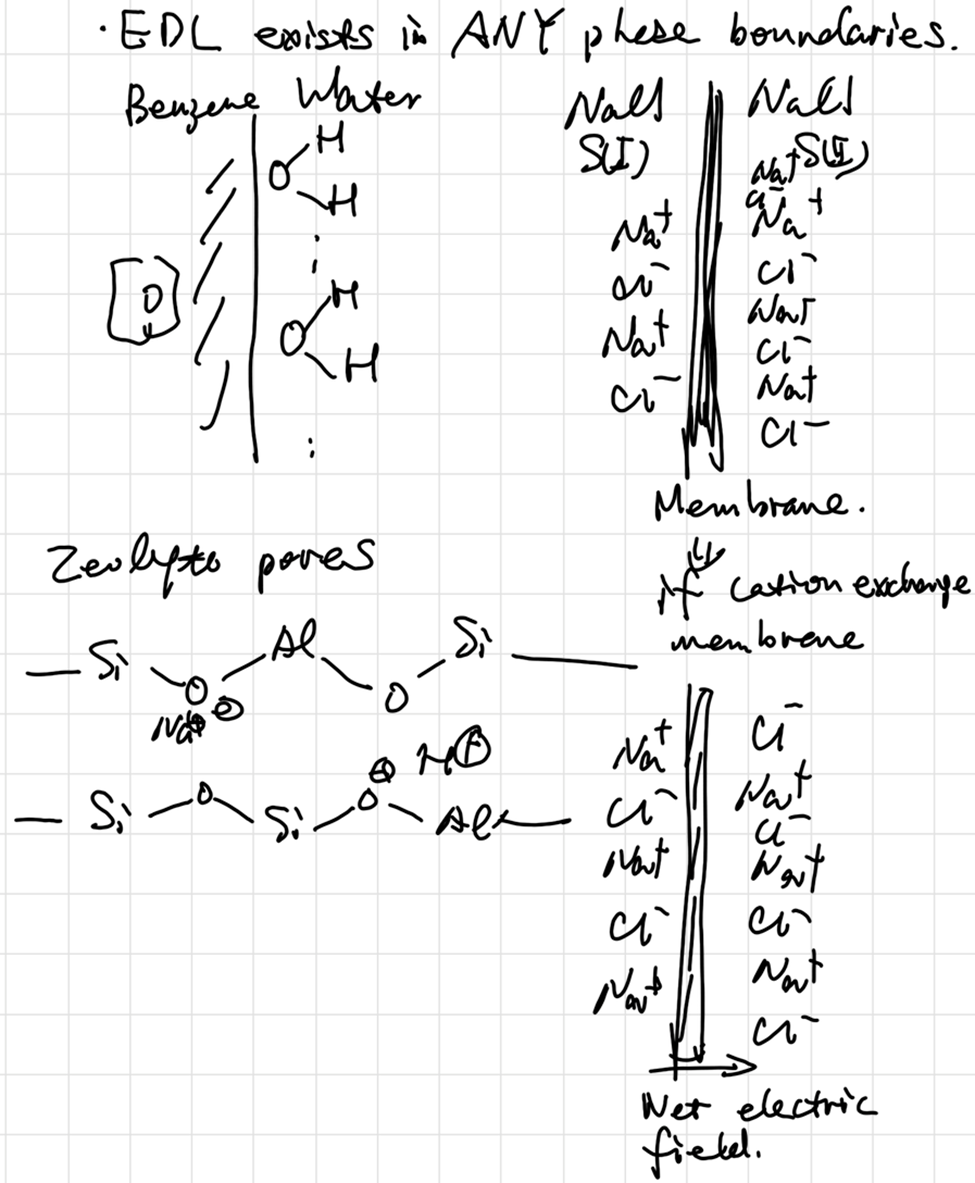
Electric Double Layer(EDL)
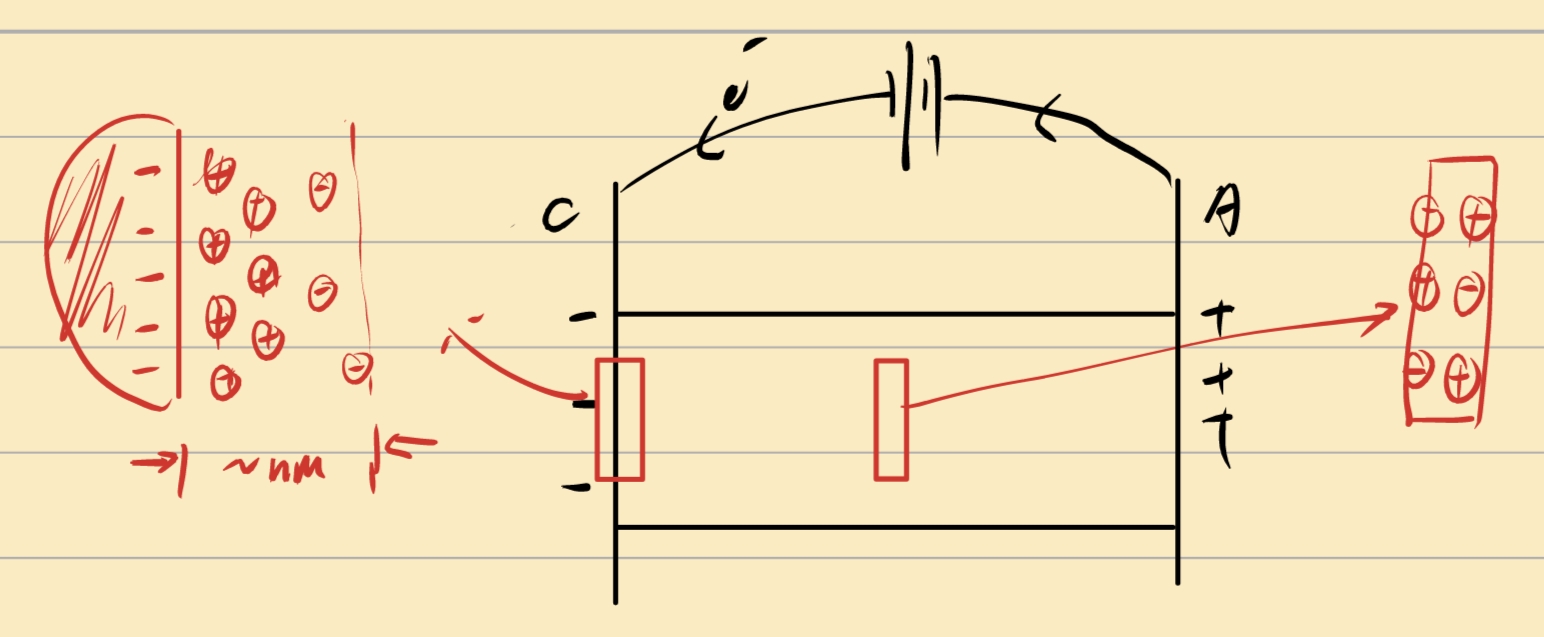
Gouy-Chapman-Stern(GCS) Model

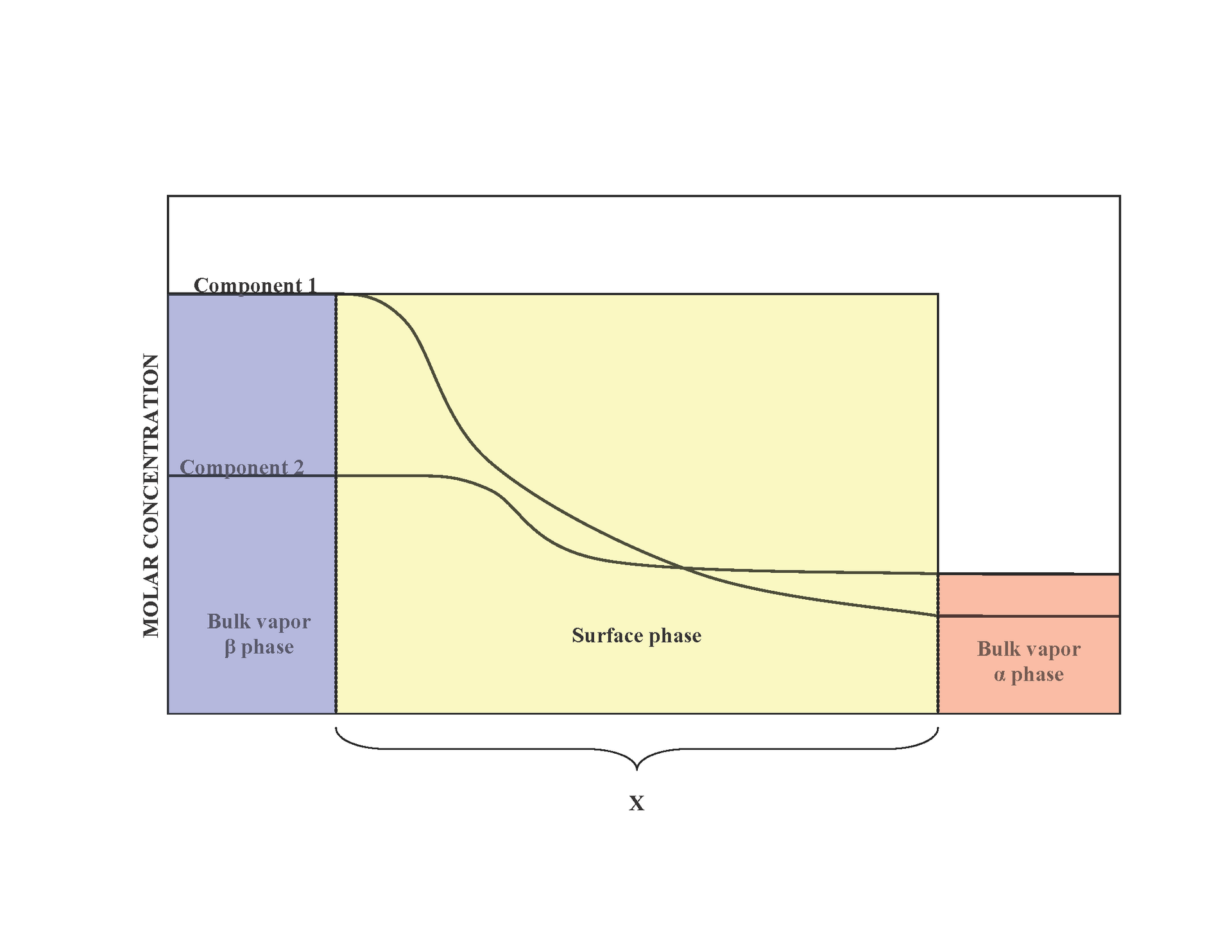
The Gibbs adsorption isotherm
Pure Phase(A) | …… | Pure Phase(B)
Reference System: (省略了偏摩尔量)
\[ \dd G_R = (\frac{\partial G_R}{\partial T})\dd T + (\frac{\partial G_R}{\partial p}) \dd p +(\frac{\partial G_R}{\partial n})\dd n \]
Actual system:
\[ \dd G_S = (\frac{\partial G_S}{\partial T})\dd T + (\frac{\partial G_S}{\partial p}) \dd p +(\frac{\partial G_S}{\partial n})\dd n + (\frac{\partial G_S}{\partial A})\dd A \]
where \(A\) indicates interfacial area, we call \(\displaystyle(\frac{\partial G_S}{\partial A})_{p,T,n} = \gamma\) as Surface Tension
As p&T are const., 认为所有物质均为纯态,即 \(\mu_i^R = \mu_i^S\),we have:
\[ \dd G^\sigma = \dd G_S - \dd G_R = \sum_i \mu_i(\dd n_i^S - \dd n_i^R) + \gamma \dd A= \sum_i \mu_i\dd n_i^\sigma + \gamma \dd A \]
\(n_i^\sigma\) is difference.
for total differential:
\[ \dd G^\sigma = \sum_i \mu_i\dd n_i^\sigma + \sum_i n_i\dd \mu_i^\sigma + \gamma \dd A + A \dd\gamma \]
that is Gibbs-Duham Relation :
\[ \begin{gathered} A\dd \gamma + \sum_i n_i^\sigma \dd \mu_i = 0 \\ -\dd \gamma = \sum_i \frac{n_i^\sigma}{A} \dd\mu_i = \sum_i \Gamma_i \dd\mu_i \end{gathered} \]
\(\Gamma\) is called Surface excess concertation( 表面过剩浓度 )
上文所说的实际上是,相对表面过剩浓度 \(\Gamma_i^1\),即认为组分 1 的表面过剩为零的平面为划分面,其不依赖于选取的分界面的位置 :
\[ \Gamma^1_1 = 0, \quad \Gamma_i^1 = \Gamma_i - \Gamma_1 (\frac{C_i^\alpha - C_i^\beta}{C_1^\alpha - C_1^\beta}) = \Gamma_i - \Gamma_1 \frac{C_i^\sigma}{C_1^\sigma} \]
we have:
\[ \begin{gathered} \dd\mu_i = RT\dd \ln fC_i \\ \Gamma_i = -\frac{1}{RT}(\frac{\partial \gamma}{\partial \ln fC_i})_{T,p} \end{gathered} \]
Electrocapillary Equation
\[ \ce{Wire---Cu'|Ag|AgCl(Ref)| K+, Cl-, M(electrolyte) |(WE)Hg|Ni|Cu---Wire} \]
for Working Electrode :
\[ \begin{aligned} -\dd \gamma &= (\Gamma_{Hg}\dd\mu_{Hg} + \Gamma_{e}\dd\mu_{e,Hg})\\ &+(\Gamma_{K+}\dd\mu_{K+} + \Gamma_{Cl-}\dd\mu_{Cl-})\\ &+(\Gamma_{M}\dd\mu_{M} + \Gamma_{H_2O}\dd\mu_{H_2O}) \end{aligned} \]
we have:
\[ \begin{cases} (\Gamma_{Hg}\dd\mu_{Hg} + \Gamma_{e}\dd\mu_{e,Hg}) = \Gamma_{e}\dd\mu_{e}^{Cu} \\ \dd \mu_{K+} + \dd \mu_{Cl-} = \dd \mu_{KCl} \end{cases} \]
for Ref Electrode :
\[ \ce{AgCl + e <--> Ag + Cl-} \]
\[ \mu_{\ce{AgCl}} + \mu_{e}^{Cu'} = \mu_{\ce{Ag}} + \mu_{\ce{Cl-}} \]
做全微分:
\[ \dd \mu_{e}^{Cu} = \dd \mu_{\ce{Cl-}} \]
代入原方程:
\[ \begin{aligned} -\dd \gamma &= \Gamma_{e}\dd \mu_{e}^{Cu} -(\Gamma_{K+} - \Gamma_{Cl-})\dd \mu_{e}^{Cu'} \\ & +\Gamma_{K+}\dd\mu_{KCl} +(\Gamma_{M}\dd\mu_{M} + \Gamma_{H_2O}\dd\mu_{H_2O}) \end{aligned} \]
where \(\sigma_M = -F\Gamma_e\), \(\sigma_S = -F(\Gamma_{K+} - \Gamma_{Cl-})\) stand for excess charge on WE and EDL
由于电中性:
\[ \sigma_M + \sigma_S = 0 \]
于是:
\[ \begin{aligned} -\dd \gamma &= -\sigma_M \frac{\dd \mu_{e}^{Cu}}{F} + \sigma_M \frac{\dd \mu_{e}^{Cu'}}{F} \\ & +\Gamma_{K+}\dd\mu_{KCl} +(\Gamma_{M}\dd\mu_{M} + \Gamma_{H_2O}\dd\mu_{H_2O}) \\ &= \sigma_M \dd E +\Gamma_{K+}\dd\mu_{KCl} + \Gamma_{M}\dd\mu_{M} + \Gamma_{H_2O}\dd\mu_{H_2O} \end{aligned} \]
由 G-D 方程:
\[ \dd \mu_{\ce{H2O}} = - \frac{x_{KCl}}{x_{H2O}} \dd \mu_{KCl} - \frac{x_{M}}{x_{H2O}} \dd \mu_{M} \]
代入:
\[ \begin{aligned} -\dd \gamma &= \sigma_M \dd E + (\Gamma_{K+} - \frac{x_{KCl}}{x_{H2O}})\dd\mu_{KCl} + (\Gamma_{M} - \frac{x_{M}}{x_{H2O}})\dd \mu_M\\ &= \sigma_M \dd E + \Gamma_{K}(H_2O)\dd\mu_{KCl} + \Gamma_M(H_2O)\dd \mu_M \\ &=\sigma_M \dd E + C \end{aligned} \]
that is Lippmann's equation:
\[ \boxed{\sigma_M =-\frac{\dd \gamma}{\dd E}} \]
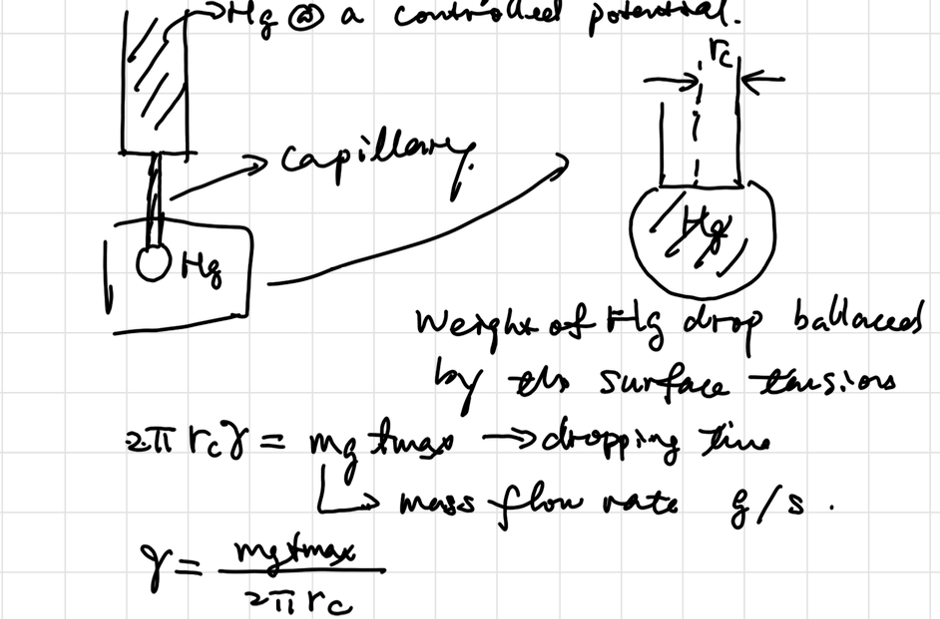
Droping Mercury Electrode
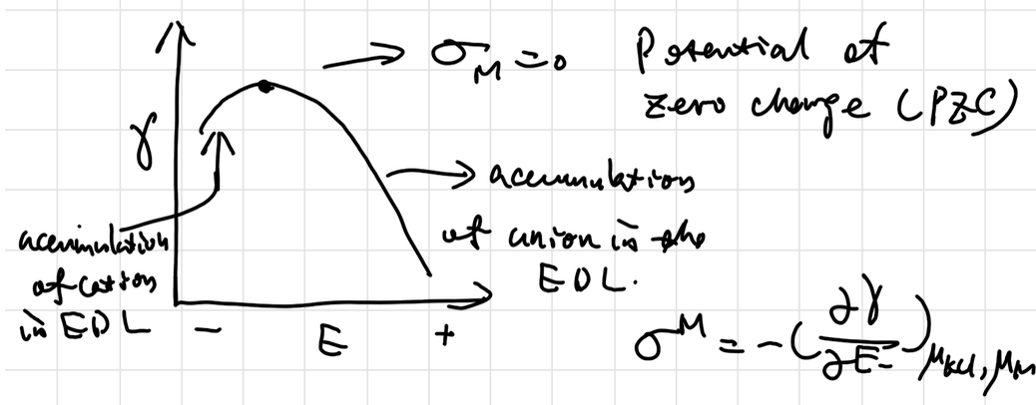
当且仅当导数为 0 时达到双电层净电荷平衡,前半段表面富集电子,排斥阴离子而吸引阳离子;后半段表面缺少电子,吸引阴离子。
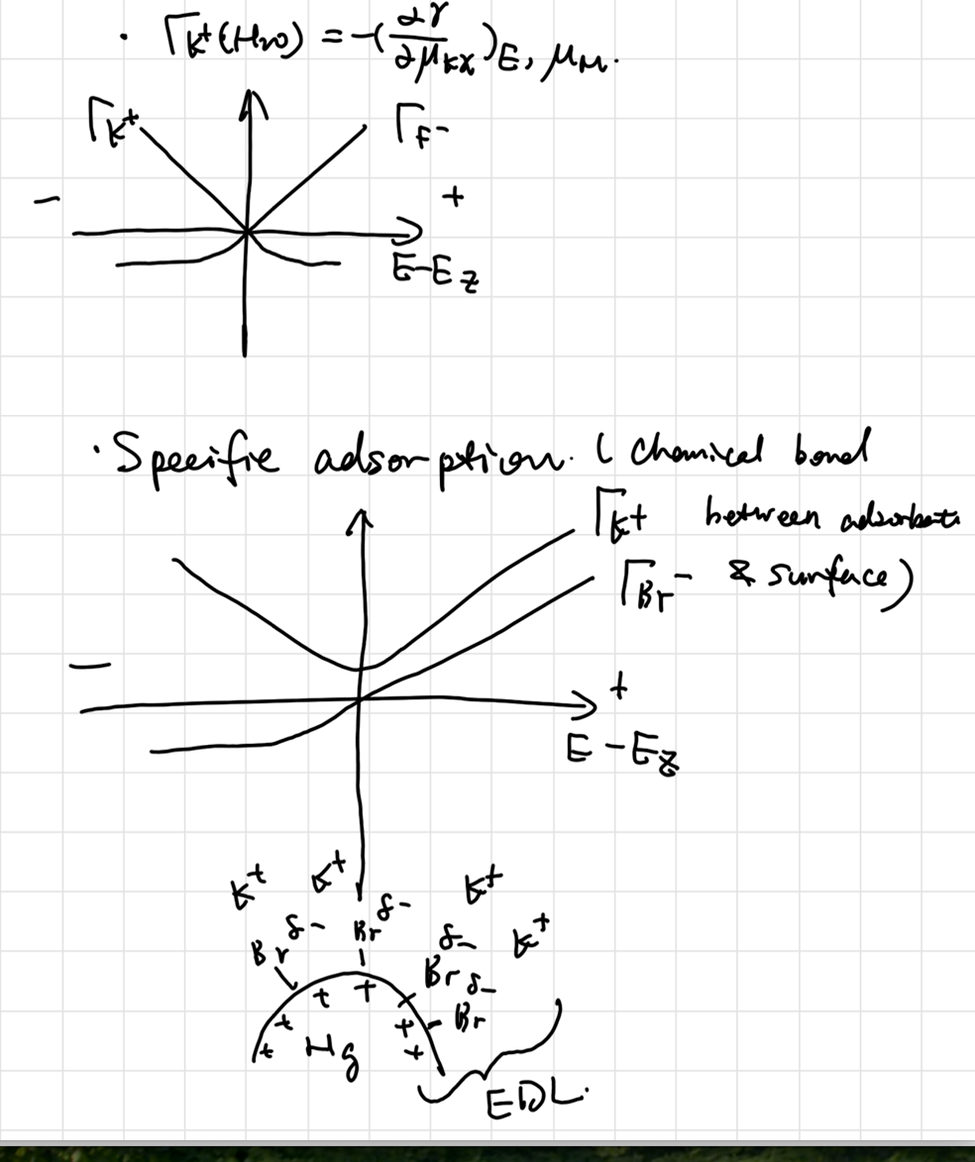
Adsorption Isotherm
\[ \begin{aligned} \mu_i^{Adsorption} &= \mu_i^{bulk}\\ \mu_i^{\circ A} + RT\ln a_i^{A} &= \mu_i^{\circ b} + RT\ln a_i^b\\ a_i^A &= a_i^be^{-\frac{\Delta G^\circ_i}{RT}} \end{aligned} \]
Assumptions:
- All surface sites are identical
- No lateral interactions
- A full coverage can be achieved
def \(a_i^A = \frac{\Gamma_i}{\Gamma_s-\Gamma_i}\), \(\theta_i = \frac{\Gamma_i}{\Gamma_s}\)
that is:
\[ \begin{gathered} \frac{\theta_i}{1-\sum\theta_i} = a_i^be^{-\frac{\Delta G_i}{RT}}\\ \theta_i = \frac{a_i^be^{-\frac{\Delta G_i}{RT}}}{1+\sum_j^N a_j^be^{-\frac{\Delta G_i}{RT}}} = \frac{a_i^b K_i}{1+\sum_j^N a_j^b K_j} \end{gathered} \]
this is Langmuir Isotherm
Including interaction among adsorbates: Frumkin isotherm
\[ a_i^be^{-\frac{\Delta G_i}{RT}} = \frac{\theta_i}{1-\sum\theta_i} \exp (-\frac{2g\Gamma_i}{RT}) \]
其中 \(-2g\Gamma_i\) 代表相互作用项。
Chapter 3 : Chemical Kinetics
Kinetic Theory of Gases KTG (Ideal Gases)
\[ p = (\frac{\partial U}{\partial V})_S \quad \text{Pressure is a measurement of energy density} \]
Assume one molecule in a \(abc\) box:
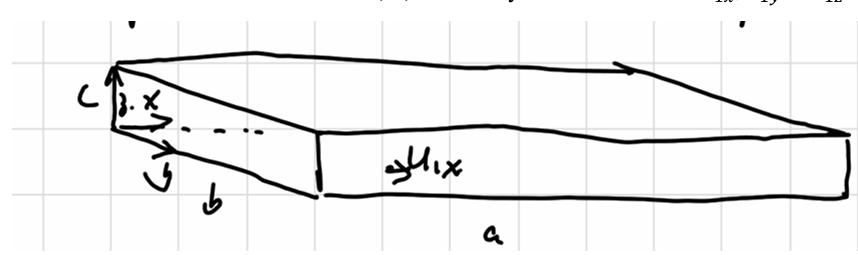
每次撞击动量改变为 \(2mu\),间隔时间为:
\[ \Delta t = \frac{2a}{u_{1x}} \]
\[ \begin{gathered} F_1 = \frac{\Delta (mu_x)}{\Delta t} = \frac{mu_{1x}^2}{a} \\ P_1 = \frac{F_1}{bc} = \frac{mu_{1x}^2}{V}\\ P = \sum_i P_i = \frac mV \sum_i u_{ix}^2 \end{gathered} \]
With symmetry \(\langle u_x^2 \rangle = \langle u_y^2 \rangle = \langle u_z^2 \rangle\)
\[ \begin{gathered} u^2 = u_x^2 + u_y^2 + u_z^2 \rightarrow \langle u^2 \rangle = \langle u_x^2 \rangle + \langle u_y^2 \rangle + \langle u_z^2 \rangle = 3\langle u_x^2 \rangle \\ PV = \frac 13 Nm\langle u^2 \rangle \\ \frac 12m\langle u^2 \rangle = \frac 32 \frac{PV}{N} = \frac 32 k_BT \\ \frac 13 M\langle u^2 \rangle = RT \end{gathered} \]
that is :
\[ \boxed{\sqrt{\langle u_x^2 \rangle} = \sqrt{\frac{3RT}{M}}} \]
let \(h(u_x,u_y,u_z)\) be the fraction of molecules with velocity between \(u_x + du_x,u_y + du_y, u_z + du_z\), as independent:
\[ h(u_x,u_y,u_z) = f(u_x) + f(u_y) + f(u_z) \]
之后利用 Boltzman 公式,然后归一化概率密度函数:
\[ \begin{gathered} f(u_x) = \sqrt{\frac{M}{2\pi RT}} e^{\frac{Mu_x^2}{2RT}}\\ h(u_x,u_y,u_z) = \left( \frac{M}{2\pi RT} \right)^\frac 32 e^{-M(u_x^2 + u_y^2 + u_z^2)/2RT} \end{gathered} \]
as polar coordinate,转化为球坐标(即在薄球壳内认为 \(\times 4\pi u^2\)):
\[ \begin{gathered} F(u)du = 4\pi \left( \frac{M}{2\pi RT} \right)^\frac 32 u^2 e^{-Mu^2/2RT} du\\ \boxed{ \langle u \rangle = 4\pi \left( \frac{M}{2\pi RT} \right)^\frac 32 \int u^3 e^{-Mu^2/2RT} du = \sqrt{\frac{8RT}{\pi M}} }\\ \langle u^2 \rangle = 4\pi \left( \frac{M}{2\pi RT} \right)^\frac 32 \int u^4 e^{-Mu^2/2RT} du = \frac{3RT}{M} \end{gathered} \]
求导可得最概然速率:
\[ u_p = \sqrt{\frac{2RT}{M}} \]
Collision of gas
assume collision in \(dt\) in the oblique cylinder,考虑能撞上面积 A 的分子数:
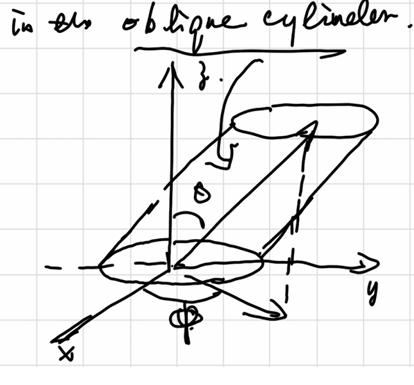
柱形内碰撞分子数等于 \(柱内分子数 \times 速度概率 \times 方向概率\)
\[ \begin{aligned} \dd N_{coll} &= \rho(Audt)\cos\theta \cdot F(u)du \cdot \frac{\sin\theta \dd\theta \dd\varphi}{4\pi} \\ \dd \xi_{coll} = \frac{\dd N_{coll}}{A \dd t} &= \rho u F(u)du \frac{\sin\theta\cos\theta \dd\theta \dd\varphi}{4\pi} \\ \xi_{coll} &= \frac{\rho}{4} \left< u \right> \end{aligned} \]
其中 \(\xi_{coll}\) 代表碰撞频率,即单位面积单位时间的碰撞次数。
Mean Free Path
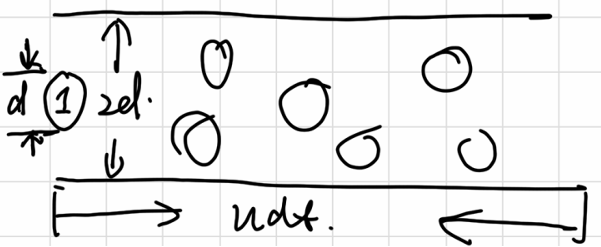
molecules in the cylinder will be collided
\[ \begin{gathered} dN_{coll} =\rho\pi d^2 \langle u_r \rangle dt \\ Z_A = \frac{dN_{coll}}{dt} = \rho\pi d^2\sqrt{\frac{8RT}{\pi \mu}} = \rho\pi d^2\sqrt{\frac{16RT}{\pi m}} \end{gathered} \]
(in dealing with two molecules relative motion)
\(Z_A\) is called collision frequency of one molecule
\[ l = \langle u \rangle dt = \langle u \rangle / Z_A = \frac{1}{\sqrt{2}\rho \pi d^2} = \frac{RT}{\sqrt{2}N_AP \pi d^2} \]
\(l\) is called mean free path
the total collision frequency \(Z\) is:(the average angle is 90° so \(u_r = \sqrt{2}u\))
\[ \begin{gathered} Z_{AA} = \frac 12 \rho Z_A = \frac12 \pi d^2 \langle u_r \rangle \rho^2 = \frac{1}{\sqrt2} \pi d^2 \langle u \rangle \rho^2\\ Z_{AB} = \sigma_{AB} \langle u_r \rangle \rho_A \rho_B = \pi\left( \frac{d_A + d_B}{2} \right)^2 ·\sqrt{\frac{8RT}{\pi \mu}}·\rho_A \rho_B \end{gathered} \]
Collision theory: \(r \propto Z_{AB}\) and rxn only happen when \(u_r > u_0\)
\[ \begin{gathered} \dd Z_{AB} \propto u_rF(u_r) = u_r^3 \exp(-\frac{\mu u_r^2}{2k_BT}) \dd u_r = Au_rF(u_r) \\ Z_{AB} = A\int_0^\infty u_rF(u_r) \to A = \sigma_{AB}\rho_A\rho_B(\frac{\mu}{k_BT})^\frac32(\frac2\pi)^\frac12 \end{gathered} \]
let \(\epsilon_r = \frac12 \mu u_r^2\) :
\[ \begin{aligned} r = \int_{\epsilon_c}^\infty dz_{AB} &= \sigma_{AB}\rho_A\rho_B (\frac{1}{k_BT})^\frac32(\frac8{\pi\mu})^\frac12 \epsilon_r \exp(-\frac{\epsilon_r}{k_BT}) d\epsilon_r \\ &= \sigma_{AB}\rho_A\rho_B(\frac{8k_BT}{\pi\mu})^\frac12(1+\frac{\epsilon_C}{k_BT})\epsilon_r \exp(-\frac{\epsilon_r}{k_BT}) \\ &= A\exp(-\frac{\epsilon_r}{k_BT})\rho_A\rho_B \end{aligned} \]
即为Arrhenius Equation
Phenomenological Kinetics
\[ \ce{\nu_AA + \nu_BB -> \nu_YY + \nu_ZZ} \]
\[ \begin{gathered} r = \frac{d\xi}{dt} = -\frac{1}{\nu_A}\frac{dn_A}{dt} = \frac{1}{\nu_Y}\frac{dn_Y}{dt} \\ r = k[\ce{A}]^{m_A}[\ce{B}]^{m_B} \\ \ln r = \ln k + m_A\ln{[\ce{A}]} + m_B\ln{[\ce{B}]} \end{gathered} \]
first/second order reactions ....
Transition State Theory:
- Reactant are in eq. with the activated complex(AC) or transition state
- AC converts to product in a irreversible step
\[ \begin{gathered} \ce{A + B <=> [AB]^\ddagger -> P} \\ K_c^\ddagger =\frac{[AB^\ddagger]c^{\circ}}{[A][B]} \end{gathered} \]
at eq \(\mu_A + \mu_B = \mu_{AB^\ddagger}\)
from statistical mechanics: \(Q = q^N / N!\)
\[ \begin{gathered} \mu = -RT(\frac{\partial \ln Q}{\partial N})_{VT} = -RT(\frac{\partial \ln {\frac{q^N}{N!}}}{\partial N})_{VT} = -RT\ln{q/N} \\ \mu^\ddagger = \mu_A + \mu_B \rightarrow \frac{q^\ddagger}{N^\ddagger} = \frac{q_A}{N_A} \frac{q_ B}{N_B}\\ \frac{N^\ddagger}{N_AN_B} = \frac{q^\ddagger}{q_Aq_B} \\ K_c^\ddagger = \frac{\frac{q^\ddagger}{V}·c_0}{\frac{q_A}{V}\frac{q_B}{V}} = \exp(-\frac{\Delta^\ddagger G ^\circ}{RT}) \end{gathered} \]
let \(\nu_c\) be the freq. at which AC cross over the barrier
\[ \begin{gathered} \frac{d[P]}{dt} = \nu_c[AB^\ddagger] = k[A][B] \\ k = \nu_c K_c^\ddagger /c^\circ \end{gathered} \]
Normal mode for the rxn
对于普通分子的三维配分函数:
\[ q_t = \frac{(2\pi mk_BT)^\frac32}{h^3} V \]
对于 AC,只有一维的平动坐标:
\[ q_t^\ddagger = \frac{(2\pi m^\ddagger k_BT)^\frac12}{h} \delta \]
平衡常数
\[ \begin{gathered} K_c^\ddagger = \frac{(2\pi m^\ddagger k_BT)^\frac12}{h} \delta \frac{\frac{q^\ddagger_{other}}{V}·c_0}{\frac{q_A}{V}\frac{q_B}{V}} \\ k = \frac{(2\pi m^\ddagger k_BT)^\frac12}{h} \delta\nu_C \frac{\frac{q^\ddagger_{other}}{V}·c_0}{\frac{q_A}{V}\frac{q_B}{V}} = \frac{(2\pi m^\ddagger k_BT)^\frac12}{h} \left< u_{AC} \right> \frac{\frac{q^\ddagger_{other}}{V}·c_0}{\frac{q_A}{V}\frac{q_B}{V}} \end{gathered} \]
在一维坐标上积分速率得到
\[ \left< u_{AC} \right> = \sqrt{\frac{k_B T}{2\pi m^\ddagger}} \]
代入即可得到:
\[ k = \frac{k_BT}{hc_0} K^\ddagger = \frac{k_BT}{hc_0} e^{-\frac{\Delta G^\ddagger}{RT}} \]
Arrhenius Equation
求导得:
\[ \begin{aligned} \dv{\ln k}{T} &= \frac 1T + \dv{\ln K_C^\ddagger}{T} \\ &= \frac 1T + \dv{T}(\frac{\Delta G^\ddagger}{RT}) = \frac 1T + \frac{\Delta U^\ddagger}{RT^2} \\ &= \frac 1T + \frac{\Delta H^\ddagger + RT}{RT^2} = \frac{\Delta H^\ddagger + 2RT}{RT^2} \end{aligned} \]
由此即可得:
\[ E_a = \Delta H^\ddagger + 2RT \]
Chapter 4: Chemical Kinetics (II)
Potential Energy Surface
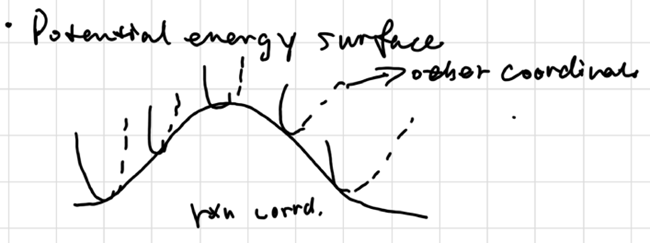
the top point of the surface is called Saddle Point
at local minimum:
\[ \frac{\partial^2u}{\partial x^2} > 0, k>0, \nu = \sqrt{\frac{\mu}{k}} \text{ is real} \]
at local maximum:
\[ \frac{\partial^2u}{\partial x^2} < 0, k<0, \nu = \sqrt{\frac{\mu}{k}} \text{ is imaginary} \]
KIE
Primary KIE
Zero Point Energy: \(E_0 = \frac 12 h\nu\) for ground state
Harmonic Approx.: \(\displaystyle{\nu = \frac 1{2\pi}\sqrt{\frac k\mu}}, \tilde{v} = \frac 1{2\pi c}\sqrt{\frac k\mu}\)
\[ \frac {\nu_{CH}}{\nu_{CD}} = \sqrt{\frac{m_Dm_C(m_D+m_C)}{m_Hm_C(m_H+m_C)}} \approx \sqrt2 \]
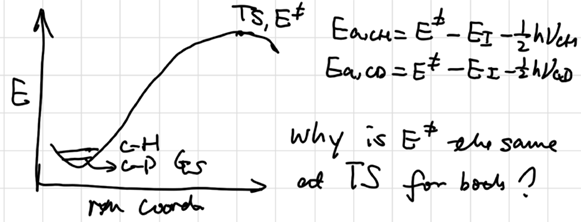
\[ \begin{aligned} \ln(\frac{k'_{CH}}{k'_{CD}}) &= \ln{\frac {A_H}{A_D}} + \frac12 \frac{h(\nu_H-\nu_D)}{k_BT}\\ \frac{k'_{CH}}{k'_{CD}} &= \exp({\frac12 \frac{h(\nu_H-\nu_D)}{k_BT}}) \approx 1\sim10 \end{aligned} \]
Secondary KIE
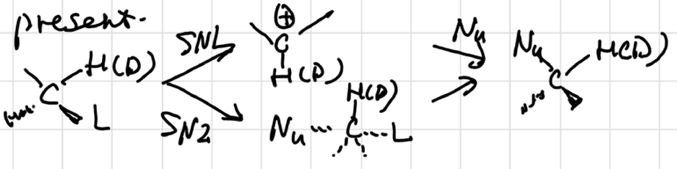
KIE: \(S_N1\) ~ 1.2, \(S_N2\) ~ 1. why?
\(S_N1\) mechanism involves a temporary increase in the bond order of C-H(D)
Early vs. Late TS
Postulates based on TST
Bronsted-Evans-Polanyi principle (BEP)
for a series of similar reactions:
\[ \Delta G_1^\ddagger - \Delta G_2^\ddagger = \alpha(\Delta G_1-\Delta G_2) \]
or
\[ \ln(k_2/k_1) = \alpha\ln(K_2/K_1) \]
where \(0<\alpha<1\)
The Hammond Postulate
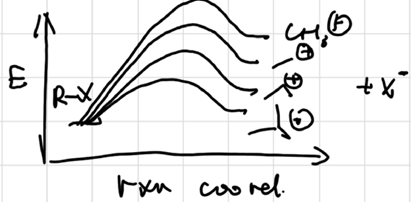
more reactive rxn will produce AC more resembles the reactant, result in less selectivity (Activity-Selectivity Principle)
The Curtin-Hammett Principle
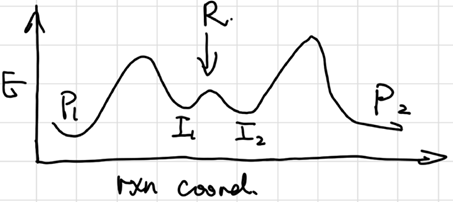
The ratio of products is determined by the relative heights of the highest energy barriers, leading to different products
Microscopic Reversibility
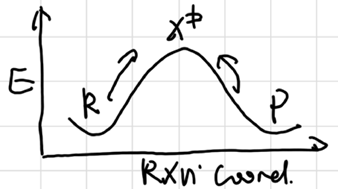
The forward and reverse rxns go identical path
Kinetic vs Thermodynamic Control
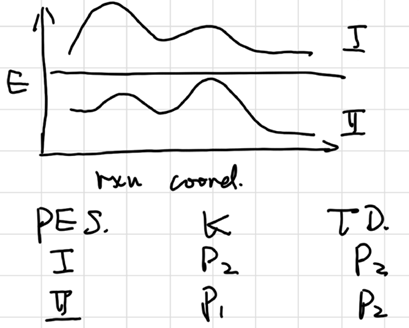
Quasi Steady Approx. (QSSA)
Key assumptions:
consider rxn:
\[ \ce{A ->[k_1] B ->[k_2] C} \]
we have:
\[ \begin{gathered} \frac{dx}{dt} = -k_1x \quad \frac{dy}{dt} = k_1x-k_2y \quad \frac{dz}{dt} = k_2y \\ \Rightarrow y = \frac{k_1}{k_2 - k_1}(e^{-k_1t} - e^{-k_2t}) \\ \frac{dy}{dt} = 0 \Rightarrow t_{max} = \frac 1{k_2-k_1}\ln{\frac {k_2}{k_1}} \\ y_{max} = \frac {k_1}{k_2-k_1}[(\frac {k_2}{k_1})^{\frac {k_1}{k_2-k_1}} - (\frac {k_2}{k_1})^{\frac {k_2}{k_2-k_1}}] \end{gathered} \]
as \(k_2\gg k_1 \Rightarrow t_{max} \to 0, y_{max} \to 0\)
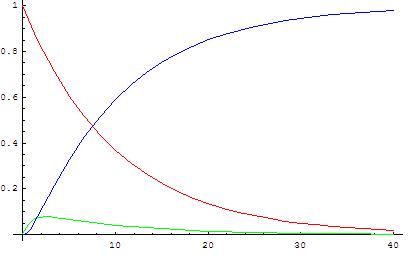
for rxns with more than one intermediates:
\[ \ce{A->[k_1]I_1 ->[k_2]I_2->...->I_n->[k_{n+1}]B} \]
all \(\ce{I_n}\) can consider into one steady state.
Pseudo-Equilibrium/ Rate limiting step
If one step has a significantly lower rate constant, then it is considered as RLS
Several steps in a row sequence could have low but comparable rate constants ⇒ kinetically relevant not RLS/RDS.
转换频率(Turnover freq.):
\[ TOF = \frac {r}{[L]} \]
Most Abundant Reaction Intermediate (MARI):
\[ \theta_i \sim 1 \]
Chapter 5: Chemical Kinetics II
RDS
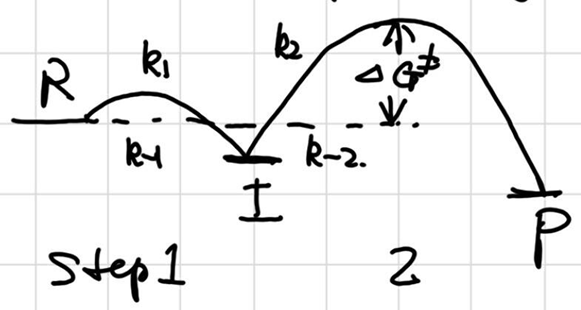
let $k_{-2} =0 $
$$ \begin{aligned} \frac{d[I]}{dt} = 0 &= k_1[R] - k_{-1}[I] - k_2 [I] + k_{-2}[P] \ &= A\exp(-\frac{\Delta G_1^\ddagger}{RT}) [R] - A\exp-\frac{\Delta G_1^\ddagger+\Delta G_1}{RT} - A\exp-\frac{\Delta G_2^\ddagger}{RT}
\end{aligned} $$
when $\Delta G_1^\ddagger + \Delta G_1 \ll \Delta G_2^\ddagger $ :
\[ \begin{gathered} \exp(-\frac{\Delta G_1^\ddagger}{RT}) [R] - \exp[-\frac{\Delta G_1^\ddagger+\Delta G_1}{RT}](I) = 0 \\ [R] = \exp[-\frac{\Delta G_1}{RT}](I)\\ r = k_2[I] = A\exp(-\frac{\Delta G_2^\ddagger}{RT})\exp[\frac{\Delta G_1}{RT}](R) \\ = A\exp[-\frac{\Delta G_2^\ddagger - \Delta G_1}{RT}](R) \end{gathered} \]
Only the highest barrier determines the rate.
Degree of Rate Control (DRC)
define the DRC of elementary step i :
\[ X_{RC,i} = \frac{k_i}{r}(\frac{\partial r}{\partial k_i})_{k_{j \neq i}, K_i} = (\frac{\partial \ln r}{\partial \ln k_i})_{k_{j \neq i}, K_i} \]
for RDS on step i :
\[ X_{RC,i} = 1, \quad X_{RC, j\neq i} = 0 \]
from TST :
$$ \begin{aligned} X_{RC,i} &= (\frac{\partial \ln r}{\partial \ln k_i}){k \ &= (\frac{\partial \ln r}{\partial \ln (\frac{k_BT}{h} \exp(\frac{-\Delta G_i^\ddagger}{RT}))})}, K_i{k \ &= (\frac{\partial \ln r}{\partial (\frac{-\Delta G_i^\ddagger}{RT})})}, K_i{k}, K_i
\end{aligned} $$
we can also define Degreee of thermodynamic controlled :
\[ \begin{aligned} X_{TC,i} &= (\frac{\partial \ln r}{\partial (\frac{-\Delta G_i}{RT})})_{k_{j \neq i}, K_i} \end{aligned} \]
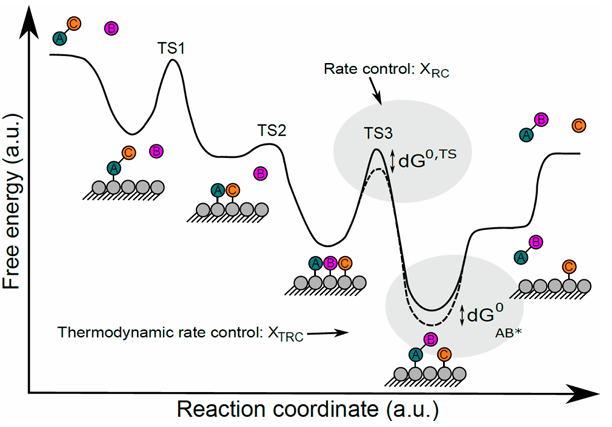
for eg:
$$ \begin{gathered} \ce{A + \ast <--> A\ast} &K_1 \ \ce{B + \ast <--> B\ast} &K_2 \ \ce{A\ast + B\ast -> AB\ast + \ast} &RDS, k_3\ \ce{AB\ast <--> AB + \ast}
\end{gathered} $$
\[ K_1 = \frac{\theta_A}{P_A \cdot \theta_*} \quad K_2 = \frac{\theta_B}{P_B \cdot \theta_B} \]
\[ \theta_A + \theta_B + \theta_* = 1 \]
若 A 为 MARI 物种: [ \theta_* = \frac{1}{P_A K_1} \quad \theta_B = \frac{K_2 P_B}{K_1 P_A} ]
\[ \tau = k_3 \theta_A \theta_B = \frac{k_3 K_2}{K_1} \frac{P_B}{P_A}= \frac{k_B T}{h} \exp \left[ -\frac{\Delta^\ddagger G_3^0 + \Delta G_2^0 - \Delta G_1^0}{RT} \right] \frac{P_B}{P_A} \]
\[ = \frac{k_B T}{h} \exp \left[ -\frac{\neq G_3^0 - \Delta G_1^0 - \Delta G_2^0 + \Delta G_2^0 - \Delta G_1^0}{RT} \right] \frac{P_B}{P_A} \]
\[ = \frac{k_B T}{h} \exp \left[ -\frac{\neq G_3^0 - 2G_A^0}{RT} \right] \frac{P_B}{P_A} \]
可得 \(X_{A,RC} = -2\),为毒化剂作用
\(X_{\ddagger,RC} = 1\) 意味着 RDS 控制反应速率
Enzymatic Catalysis
Michaelis Manton kinetics
\[ r = \frac{r_{max}[S]}{K_m + [S]} \]
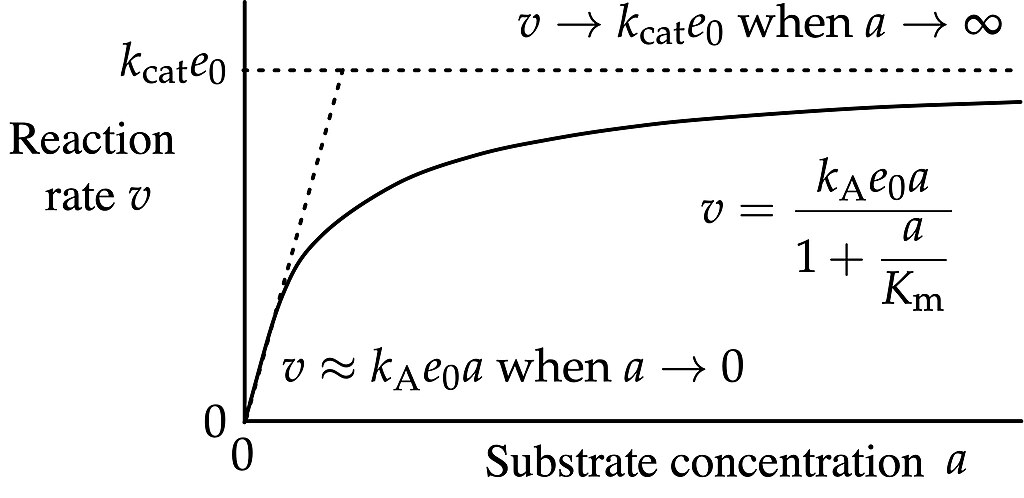
Reaction with 2 substates:
\[ \begin{gathered} E+S_1 \rightleftharpoons ES_1 &K_1\\ E+S_2 \rightleftharpoons ES_2 &K_2\\ ES_1+S_2 \rightleftharpoons ES_1S_2 &K_3\\ ES_2+S_1 \rightleftharpoons ES_1S_2 &K_4\\ ES_1S_2 \rightarrow E+P &K_5\\ K_1 = \frac{[E][S_1]}{[ES_1]} \quad K_2 = \frac{[E][S_2]}{[ES_2]} \\ K_3 = \frac{[ES_1][S_2]}{[ES_1S_2]} \quad K_4 = \frac{[ES_2][S_1]}{[ES_1S_2]} \end{gathered} \]
solve :
\[ r = \frac{k[E_0]}{1+\frac{k_4}{[S_0]} + \frac{k_3}{[S_2]} + \frac{k_2k_4 + k_2k_3}{[S_1][S_2]}} \]
Assuming \([S_2]\) is large :
\[ r = \frac{\frac{k[E_0][S_2]}{[S_2]+K_3} \cdot [S_1]}{\frac{K_1K_3 + K_4[S_2]}{[S_2]+K_3}+[S_1]} = \frac{k[E_0][S_1]}{K_4 + [S_1]} \]
Kinetics in thermal dynamically non-ideal systems
\[ \ce{A + B <--> X^\ddagger -> P} \]
应用艾琳方程:
\[ r = \frac{k_BT}{h}c_x^\ddagger = \frac{k_BT}{h}k^\ddagger \frac{\gamma_A \gamma_B}{\gamma^\ddagger} c_Ac_B \]
we have Broused-Bjerrum relation
\[ k = k_1\frac{\gamma_A \gamma_B}{\gamma^\ddagger} \]
Reaction is dilute electrolytes
\[ \lg \frac{k}{k_0} = -cZ_A^2\sqrt{I}-cZ_B^2\sqrt{I}+c(Z_A+Z_B)^2\sqrt{I} = 2cZ_AZ_B\sqrt{I} \]
if \(Z_A\) or \(Z_B = 0\) ,\(k = k_0\)
环己烯的氢气加成
on Pt:
H₂(g) ⇌ H₂(l) // 溶解
H₂(l) ⇌ H₂(p) // p: 物理吸附于表面
H₂(p) + ** → 2H* (k₃) // **RDS:氢分子解离**
\[ \begin{aligned} r &= \frac{k_BT}{h} k^\ddagger \frac{\gamma_{H2}^p}{\gamma^\ddagger} c_{H2}^p \\ &= \frac{k_BT}{h} K_Hk^\ddagger \frac{\gamma_{H2}^l}{\gamma^\ddagger} c_{H2}^l \end{aligned} \]
由于放热步骤,可认为过渡态和 H2 活度系数相近。于是 \(r \propto K_H c^l_{H2}\) 依赖于溶剂。
on Pd:
H₂(g) ⇌ H₂(l) ⇌ H₂(p) ⇌ 2H* (快速平衡)
RH* + H* ⇌ X^\neq → RH₂** (k₆ₐ, **RDS:表面加氢**)
\[ \begin{aligned} r &= \frac{k_BT}{h} k^\ddagger \frac{\gamma_{RH*}c_{RH*}\gamma_{H*}c_{H*}}{\gamma^\ddagger} \\ &= L\frac{k_BT}{h} k^\ddagger \frac{\gamma_{RH*}}{\gamma^\ddagger}\sqrt{K_H^1p_{H2}a_{**}} \end{aligned} \]
RH 为 MARI 物种,其物理状态受金属表面作用支配而与溶剂无关。
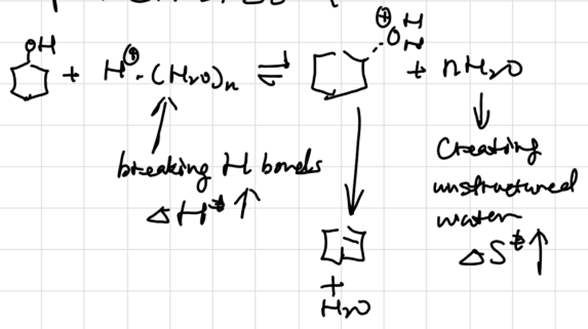
补偿效应
- 分解反应活化熵增加而活化焓也增加
- 缩合反应活化熵减小而活化焓也减小
焓熵相互补偿,导致 \(k\) 变化不大。考虑水合:
反应器
间歇式反应器 Batch
- 系统类型:封闭系统。
- 混合方式:投料时瞬间混合,反应过程中无混合。
- 浓度特征:所有组分的浓度随时间不断变化。不存在真正的稳态。
- 应用:常用于小批量、多品种的生产,如制药、精细化工。
连续搅拌釜式反应器 Continuously stirred tank reactor
- 系统类型:开放系统。
- 混合方式:瞬间、全混。进料一进入 CSTR,其组成立即与釜内及出口物料完全相同。
- 浓度特征:釜内各处浓度均匀,且不随时间变化(稳态),但等于出口的低浓度。
- 应用:适用于对返混要求不高的反应,易于控制温度和连续操作。
活塞流反应器l Pug-flow reaction
- 系统类型:开放系统。
- 混合方式:在垂直于流动的方向上无混合;在沿流动的方向上无混合。流体像“活塞”一样向前推进。
- 浓度特征:反应物浓度沿反应器长度方向逐渐降低。在任一特定截面上,组成是均匀的。
- 应用:适用于要求高转化率的反应,因为它避免了返混导致的效率下降,是工业上最常用的反应器类型之一。
Chapter 6 Electrode Kinetics
Electro Kinetics
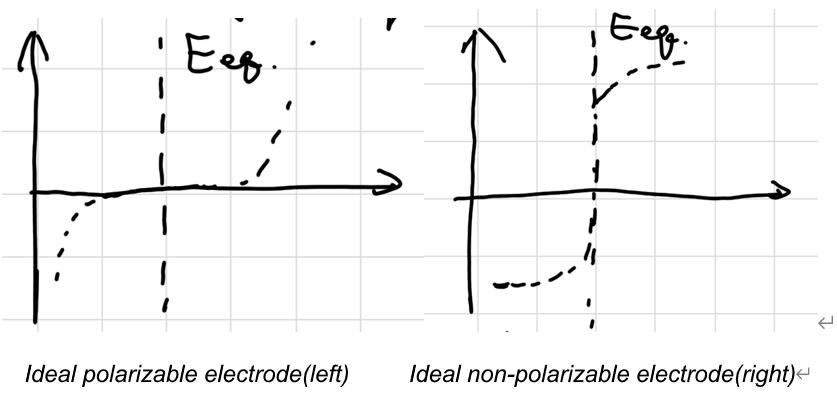
理想可极化电极:不允许电子通过,只能积累电荷,电极本身不发生电化学反应,如惰性电极
理想不可极化电极:允许电子通过,反应快且电位基本不变,如参比电极
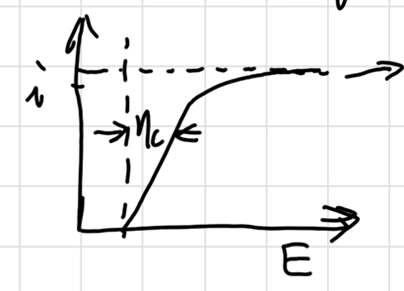
实际存在过电位:
\[ \eta = E - E_{eq} \]
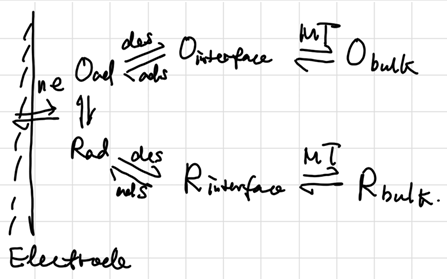
Semi-empirical Steady-State Treatment
扩散层:假定电极附近有一段无法搅拌的,厚度为 \(\delta\) 的停滞层(stagnant layer),其浓度是线性减小的:
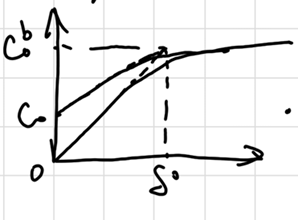
\[ v_{mt} = D_O (\dv{C_O}{x})_{x=0} = D_O \frac{C_O^b - C_O}{\delta_O} = m_O(C_O^b - C_O) \]
where \(m = D / \delta\) stands for 质量传递系数(mass transfer coef.). 若认为单位时间的扩散通量可用电流表示:
\[ \frac{i}{nFA} = m_O(C_O^b - C_O) = m_R(C_R - C_R^b) \]
当 \(C_O = 0\) 时达到极限电流:
\[ i_l = nFAm_OC_O^b, \quad \frac{C_O}{C_b} = 1-\frac{i}{i_l}, \quad E = E^{\circ\prime} + \frac{RT}{nF}\ln\frac{i_l-i}{i_l} \]
if R initially absent:
\[ \begin{gathered} C^b_R = 0, C_R = \frac{i}{nAFm_R} \\ C_O = (1-\frac{i}{i_l})\frac{i_l}{nAFm_O} \\ E = E^{\circ\prime} - \frac{RT}{nF} \ln \frac{m_O}{m_R} + \frac{RT}{nF} \ln \frac{i_l - i}{i_l} \end{gathered} \]
令半波电位 \(i = i_l/2\):
\[ E_{1/2} = E^{\circ\prime} - \frac{RT}{nF} \ln \frac{m_O}{m_R} \]
可反映相对扩散速率
id R is isolable:
\[ \begin{gathered} a_R = 1 \\ E = E^{\circ\prime} + \frac{RT}{nF}\ln C_O = E^{\circ\prime} + \frac{RT}{nF}\ln\frac{i_l-i}{i_l} + \frac{RT}{nF}\ln{C_O^b} \end{gathered} \]
when i=0, \(C_O = C_O^b\):
\[ E_eq = E^{\circ\prime} +\frac{RT}{nF}\ln{C_O^b} \]
于是过电位:
\[ \eta = |E-E_{eq}| = |\frac{RT}{nF}\ln\frac{i_l-i}{i_l}| \]
Electrode kinetics
Tafel Equation:
\[ \eta = a+b\log i \]
b:Tafel 斜率 (mV/dec),表示电流增一数量级所需的电位变化
Bulter-Volmer Kinetics
Chapter 5: Phase Diagrams
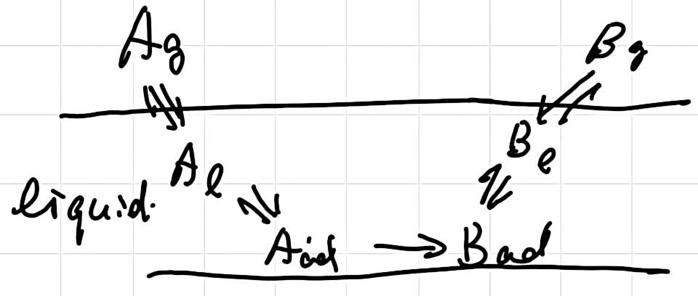
Liquid-Solid diagram
Canonical ensemble 正则系综
define
\[ \alpha = -\frac{\mu}{kT}, \beta = \frac 1{kT} \]
we have mixing entropy( 用概率代替浓度 ):
\[ S = -k\sum_I f_i\ln f_i \]
and two condtrains:
\[ \begin{cases} \sum_i f_i = 1 \\ \sum_i f_i E_i = U \end{cases} \]
when reaching maximum entropy, we can derive: 他妈了隔壁的我不会推导
\[ f_i = \frac{e^{-\beta E_i}}{\sum_ie^{-\beta E_i}} = \frac{e^{-\beta E_i}}{Z(V,T,N)} \]
where \(Z(V,T,N)\) 是正则配分函数
在这里用离散和是不精确的,我们改成积分形式。by using H, for single partical:
\[ Z = \frac{1}{h^3} = \int e^{-\beta H(\vec x,\vec p)} d^3\vec x d^3\vec p \]
and for many partials:
\[ Z = \frac{1}{h^{3N}} \int \prod_{i=1}^{N} e^{-\beta H(\vec x_i , \vec p_i)} d^{3N}\vec x_i d^{3N} \vec p_i \]
if particals are 全同:
\[ Z = \frac{1}{N!h^{3N}} \int \prod_{i=1}^{N} e^{-\beta H(\vec x_i , \vec p_i)} d^{3N}\vec x_i d^{3N} \vec p_i \]
这些即认为最小的单位空间是 \(\frac 1h\),把 N 个粒子分配到这些空间里。
通过配分函数计算能量的期望值:
\[ \begin{aligned} \left< Z \right> = \sum_i E_iP_i &= \frac1Z \sum_i E_ie^{-\beta E_i}\\ &= -\frac1Z \frac{\partial}{\partial\beta} Z(\beta, E_i) \\ &= -\frac{\partial \ln Z}{\partial \beta} = kT^2\frac{\partial \ln Z}{\partial T} \end{aligned} \]
进而还可得出自由能的关系,我们有:
\[ \begin{gathered} S = -k\sum f_i \ln f_i = -\frac kZ\sum (-\beta E_i - \ln Z)e^{-\beta E_i} = k(\ln Z + \beta\left< E \right>) \\ \left< E \right> = U \\ F = U-TS = -kT\ln Z \end{gathered} \]
巨配分函数 \(\Xi\):
\[ \Xi(\mu, V,T) = \sum_{N=0}^\infty Z(N,V,T) \lambda^N = 1+\sum_{N=1}^\infty Z(N,V,T) \lambda^N \]
where \(\lambda = e^{\beta\mu}\) represent absolute acivity(绝对活度)