Lecture 1: 晶体学基础与对称性¶
约 8725 个字 64 张图片 预计阅读时间 29 分钟
1.1 晶胞与宏观晶体¶
1.1.1 晶胞的选取¶
众所周知,晶胞指的是晶体中可以通过平移无限延展的一种重复单元,一般由一个几何体以及其内部填充的原子组成。需要注意的是,一个晶胞不仅需要包含其内部的原子,还需要包含几何体内的空间,这意味着构成晶胞的几何体必须仅通过平移形成二维或三维密铺。
在二维情况,这类的情况有很多,主要包括以下两种结构的衍生:
| 平行四边形(包括正方形,矩形,菱形等) | 含有对称中心的六边形 |
|---|---|
 |  |
不难看出,对于二维结构而言,其共同含有对边平行且相等的特征,不妨称为平行多边形(parallelogon)。我们把这一特征运用的三维情况下,可以构造出如下平行多面体(parallelohedron):
| 平行六面体 | 截角八面体(\(4^66^8\)) | 菱形十二面体() | 拉长十二面体 | 中心对称六棱柱 |
|---|---|---|---|---|
 |  |  |  |  |
 |  |  |  |  |
形如 \(4^66^8\) 的记号被称为多面体记号(正式的叫施莱夫利符号,严格来说数学上并没有这样的写法,但是竞赛里一般都用这种写法表示),表示一个多面体由6个四边形面和8个六边形面组成。
一般而言,这样的多面体选取越简单越好,于是乎人们规定二维晶胞的形状为平行四边形,三维晶胞的形状为平行六面体。
常见的平行六面体晶胞分为两种:
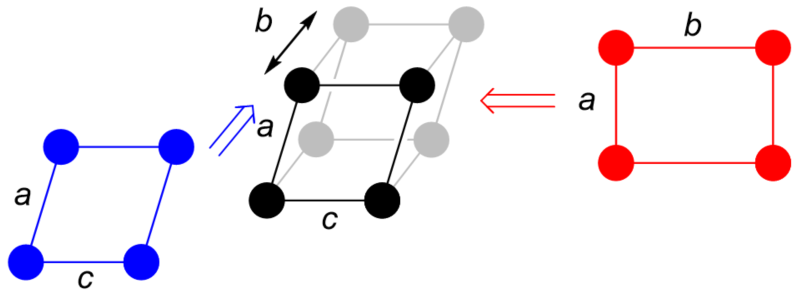
- 素晶胞(primitive cell,也叫原胞):恰好只包含一个点阵点的晶胞,即所选的晶胞恰好是一个最小的重复单元,对平行六面体的具体形状没有要求。
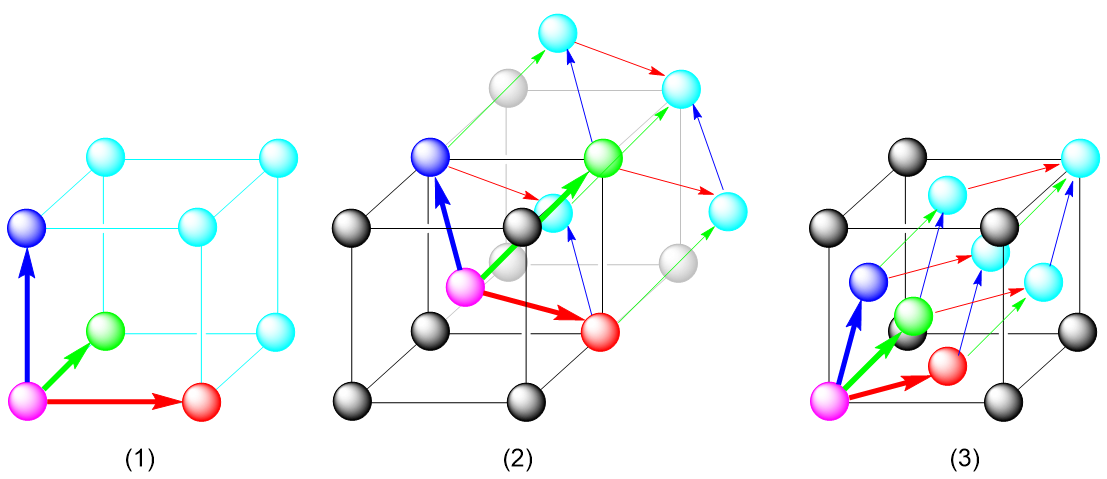
习惯上对于素晶胞,常常选择一个点阵点作为顶点,这样方便定位。对于平行六面体而言,只需确定其棱边上的三个向量 \(\vec{a}, \vec{b}, \vec{c}\) 即可确定其在空间内的位置,所以我们只需要先找到一个点阵点,再在它周围选择其他三个点阵点构建向量,最后由平移对称性即可构建整个素晶胞。
- 正当晶胞(conventional cell):
正当晶胞是为了更便捷的研究晶体的对称性取出的晶胞,因此引入了允许带心晶胞的概念(我们之后介绍),使晶胞整体呈现更加对称的形状。满足所谓“三原则”:
- 完全反映点阵的对称性;
- 包含尽可能多的直角;
- 体积尽量小(但不一定是最小)。
一般而言,通常说的“晶胞”都指的是反映对称性的正当晶胞。
除此以外还有超晶胞(supercell)的概念,即由多个正当晶胞叠加形成的晶胞 ,通常只是作为计算或构建模型的辅助工具。
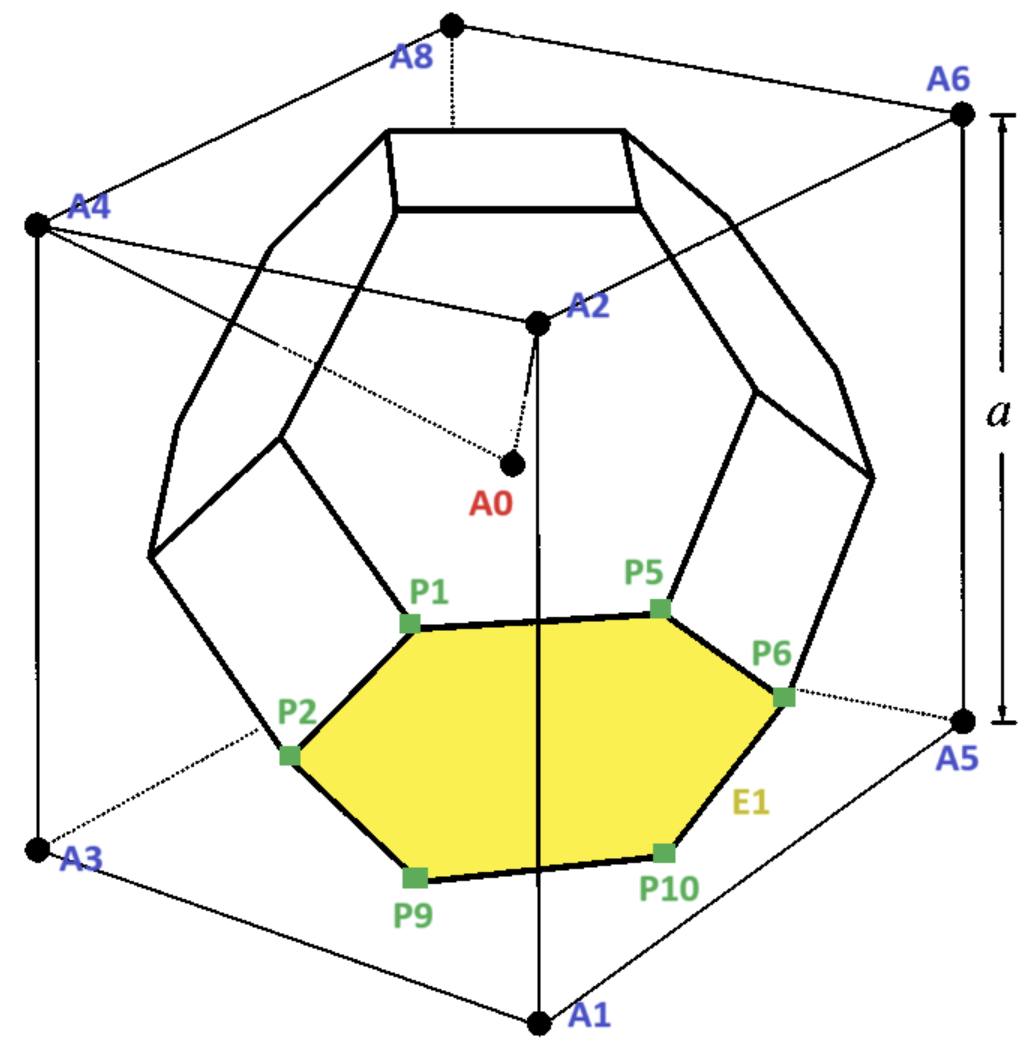
拓展:维格纳-赛茨原胞(Wigner–Seitz cell)
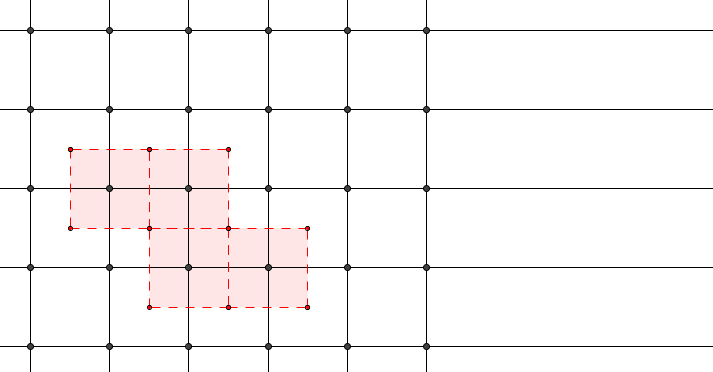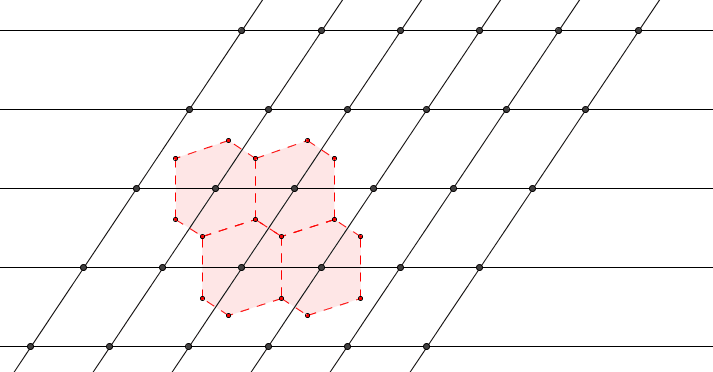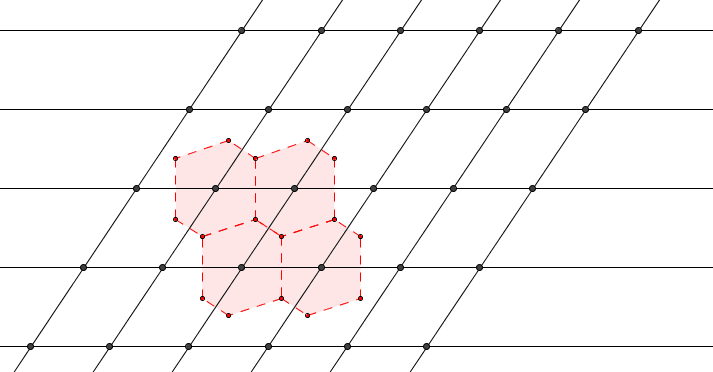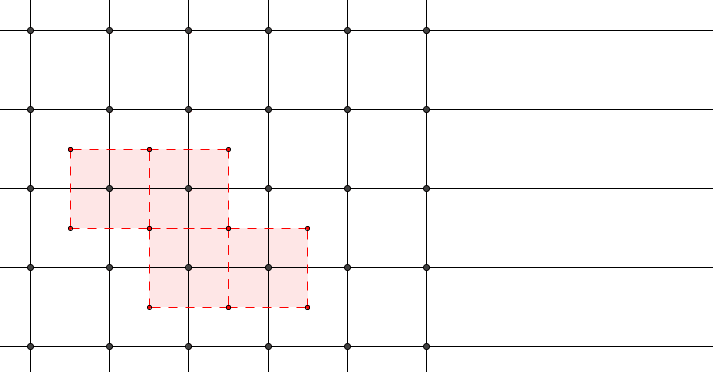
物理学家创造了一种特殊的原胞,其通过画出一个点阵点与周围相邻点阵点连线的垂直平分线围出。它同样满足平移密铺,且只含一个点阵点,但是并不一定是平行四边形:
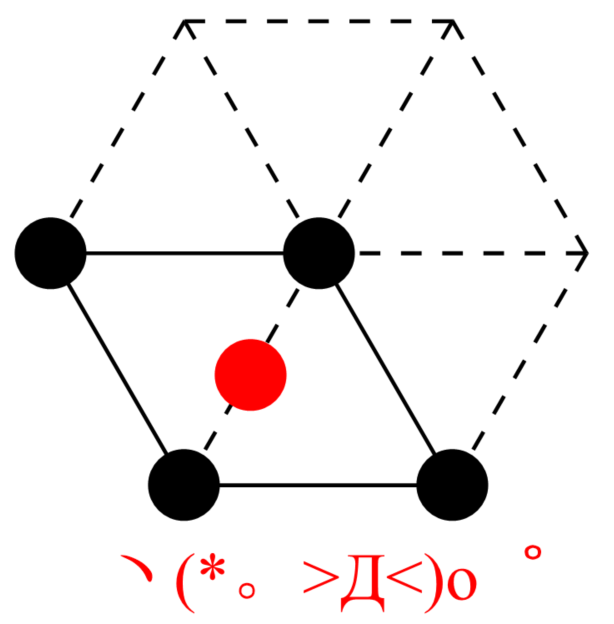
在三维空间里也是同理,我们需要画出一个点阵点与周围相邻点阵点连线的垂直平分面,围出的立体图形即为维格纳-赛茨原胞。对于体心立方点阵和面心立方点阵而言,其对应的维格纳-赛茨原胞原胞分别为截角八面体和菱形十二面体。
| 体心立方-截角八面体 | 面心立方-菱形十二面体 |
|---|---|
 |  |
1.1.2 晶面与晶向¶
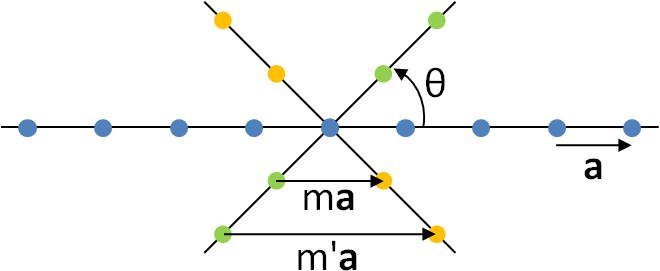
我们考虑一个立方体晶胞中的一个面:
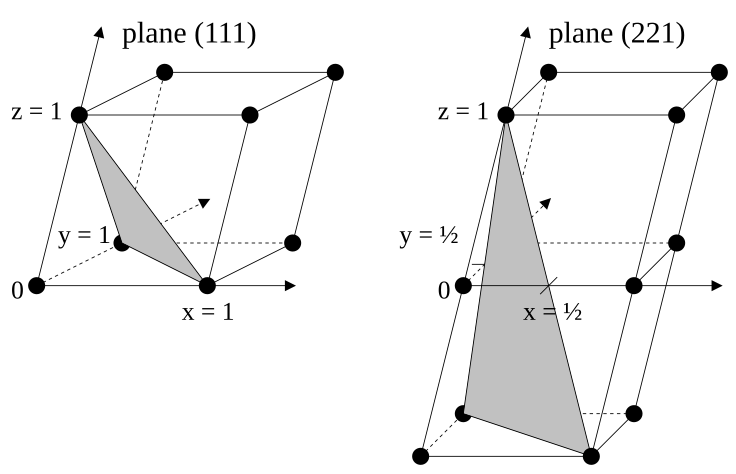
显而易见的,他与三个坐标轴的交点为 \(a, b, c\) ,因此我们可以用着三个数值表示这个晶面。但是如果是这样呢?
此时这个晶面在 \(c\) 轴上没有交点,此时再想用上面那种方法表示就难了。于是我们不妨不直接用截距表示,而是用截距的倒数表示,定义:
我们就可以用 \((hkl)\) 来代表一个晶面,这样就可以利用 \(0 = 1/\infty\) 把无穷远点消除掉。例如,上面这种晶面就可以表示为 \((\frac 1a, \frac 1b, 0)\) ,这样的定义方法叫做Miller 晶面指数。这样的定义方法对于其他形状的晶胞也是适用的。
更多晶面指数
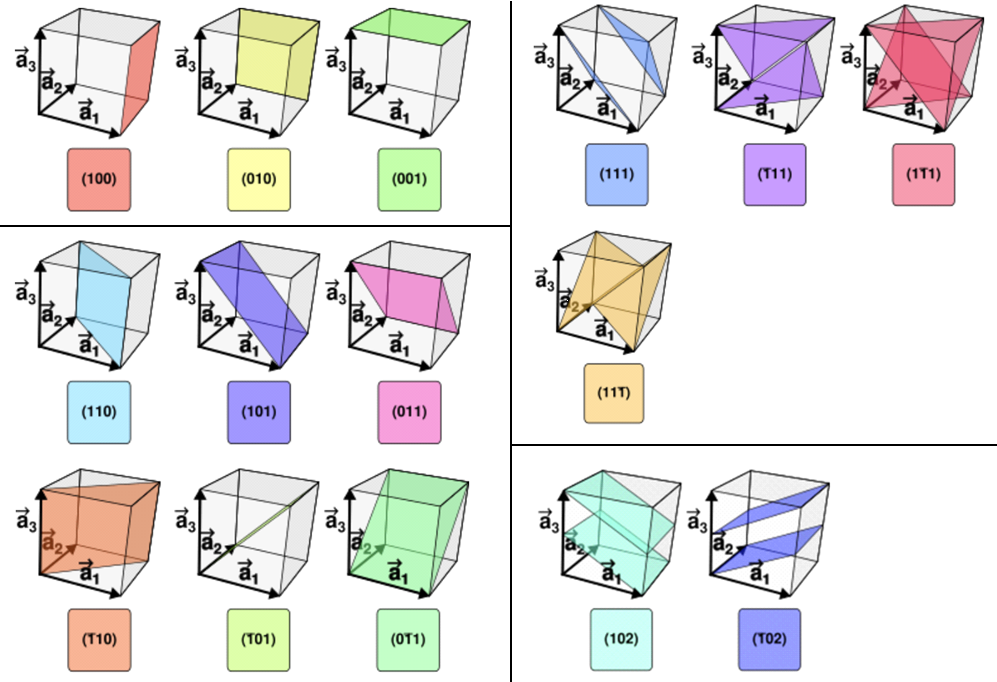
一般而言,在晶体学里的 \(-1\) 常常用 \(\overline{1}\) 表示,由此可以延申出各个取向的晶面。符号相同的晶面都是互相平行的:
对于立方晶胞,由于其对称性,\((100)\), \((010)\) 和 \((001)\) 的环境其实是一样的。为了方便起见,我们可以把它们设成一个集合 \(\{100\}\) ,这便称为一个晶面族。同理我们还有 \(\{110\}\) 晶面族和 \(\{111\}\) 晶面族。
学过高中数理都知道,平面实际上是有方向的,不过我们一般只在向量运算中讨论。所以,如果严格讨论晶面的取向,晶面 \((100)\) 应当具有指向前方和指向后方两种向量,我们可以分别记为 \([100]\) 和 \([\overline{1}00]\) 。这被称为晶向指数。
同样的,晶向指数形成的族称为晶向族指数,用尖括号括起来,例如 \(\left<100\right>\) 代表的是 \([100], [\overline{1}00], [010], [0\overline10], [001], [00\overline1]\) 六个晶向指数的集合。
总结
| 名称 | 符号 | 描述对象 | 核心含义 | 举例(立方晶系) |
|---|---|---|---|---|
| 晶面指数 | \((hkl)\) | 单个晶面 | 表示一组特定的、相互平行的原子平面。 | (100):与a轴垂直的平面。 |
| 晶面族指标 | \(\{hkl\}\) | 所有等效晶面 | 表示由晶体对称性联系起来的、性质相同的一组晶面。 | {100}:包括\((100), (010), (001)\)的所有立方体表面。 |
| 晶向指数 | \([uvw]\) | 单个晶向 | 表示晶体中的一个方向。 | [100]:沿着a轴的方向。 |
| 晶向族指数 | \(\left<uvw\right>\) | 所有等效晶向 | 表示由晶体对称性联系起来的、性质相同的一组晶向。 | <100>:包括\([100], [\overline{1}00], [010], [0\overline10], [001], [00\overline1]\)的所有立方体棱边方向。 |
1.1.3 晶体生长与宏观晶体¶
现在我们来研究关于宏观晶体的性质。
由于实际晶体不能满足平移对称性(否则整个空间就全是晶体了),所以不可避免的会产生形状。早期科学家通过对晶体的研究,确认了其具有以下性质:
- 二面角守恒定律:同种晶体在相同条件下结晶,其相邻晶面夹角总是保持一个恒定的值;
- 各向异性:晶体的热传导性质,力学性质等在不同方向上存在差异;
- 自范性:人为改变晶体形状后使之在饱和溶液中继续结晶,晶体会重新生长成多面体形;
- 均匀性:晶体内部的微观结构始终是均匀的,使之具有恒定的熔点。
观察这些性质,不难发现:宏观晶体的表面和微观晶胞的晶面存在关系。
事实上,宏观晶体的表面正是微观结构中某些晶面的对应,如何找出其对应关系呢?我们从晶体的生长考虑:晶体生长无非就是原子/分子靠近并沉积在晶面上的过程,因此,如果各个晶面上的沉积速度相同,晶面上原子密度更大者,相同时间内沉积的层数就越小,进而生长速度也越小。在最终晶体的形状上,生长快的晶面会消失,而生长最慢,也就是原子密度最大的晶面会被保留下来。这一规律被称为布拉维法则(Bravais' Rule)。
下图演示了这一沉积过程, \(BC\) 晶面生长速度快而更快消失。
哪些晶面容易形成晶体表面呢?通常是低指数的晶面,因为其通常具有较低的原子密度。对于高指数晶面而言,其通常具有较大的表面积,因此其生长速度也是相当快的。
另一种理解方式
我们也可以从吉布斯自由能变理解。晶体生长时需要满足最低的吉布斯自由能,而晶体本身的自由能包括内部能量和表面能两部分。在表面能上,原子密度越大的晶面,原子间的相互作用力越强,致使其在最终宏观晶体上得以体现。
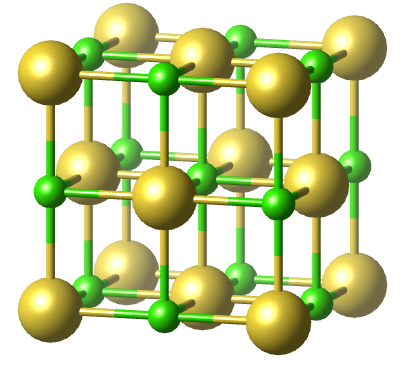
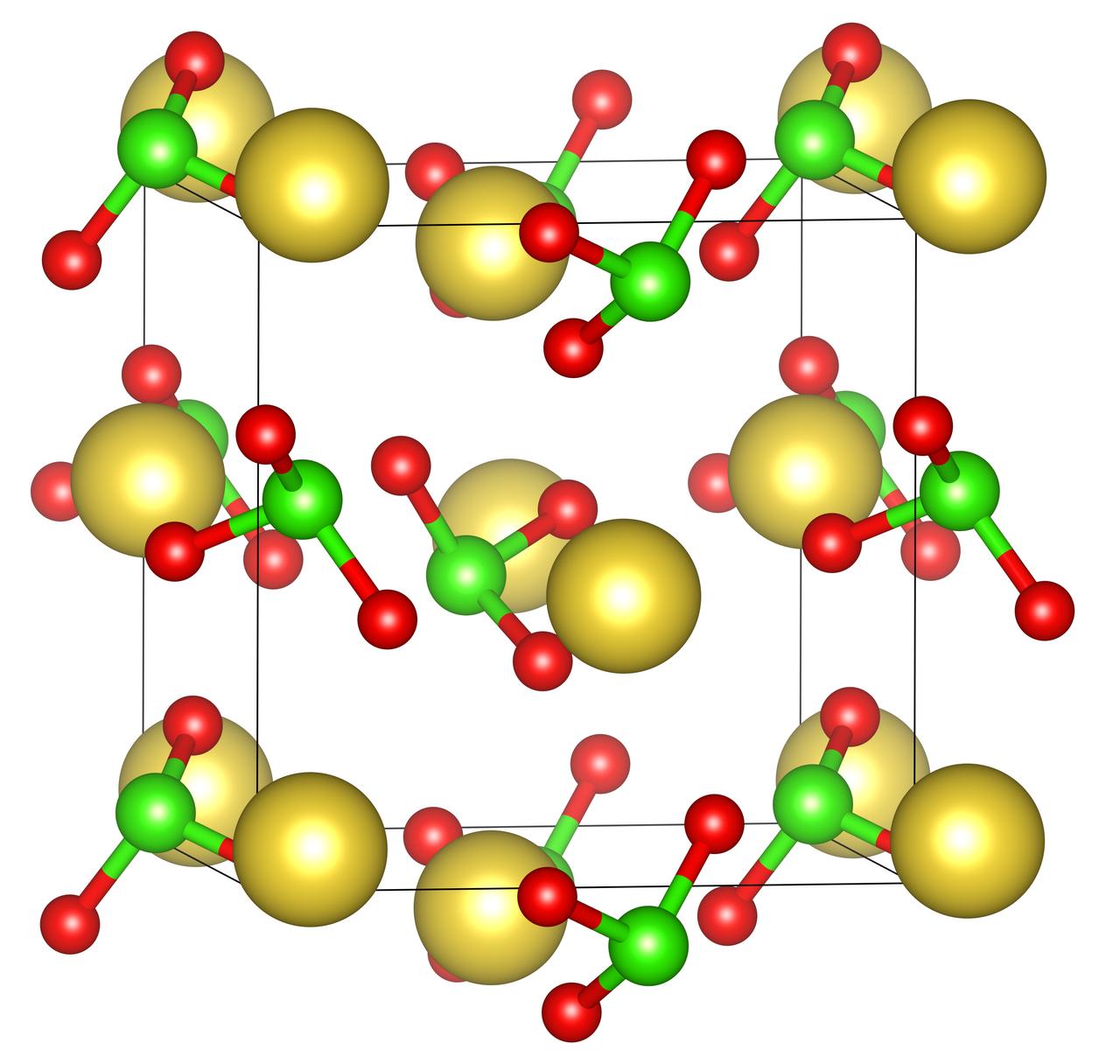
以氯化钠晶体作为例子,我们来看看布拉维规则的运用。
氯化钠的晶型
已知氯化钠晶体如下图所示,根据布拉维法则判断其宏观晶体形状。
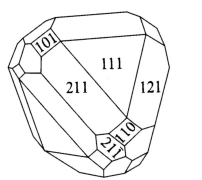
以立方晶系为例子,从最低指数的晶面开始考虑, \(\{100\}\) 族对应立方体形,而 \(\{111\}\) 族对应着沿体对角线的八个晶向生长的晶面,不难想出其对应八面体形,一个典型的例子是明矾晶体。 \(\{110\}\) 族则对应沿体心到棱形延申的12个晶向生长的晶面,形状有些复杂,对应的是菱形十二面体形。
从这三种基础模式,我们可以延伸出更多“杂交”的晶形:
实际晶体的结构远比上面介绍的更加复杂,往往会体现更多的晶面,例如黝铜矿(\(\ce{Cu3SbS3}\)):
| 黝铜矿的晶面 | 黝铜矿的宏观晶体 |
|---|---|
 |  |
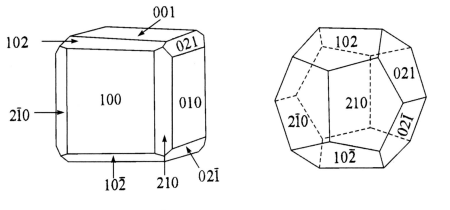
一个有趣的例子是黄铁矿。在黄铁矿的宏观晶体里,常常同时体现 \(\{100\}\) 和 \(\{210\}\) 两个晶面族,前者对应6种晶向,后者对应12种晶向。当后者在主体结构中占上风时。会形成类似五角十二面体的结构;然而晶体中并不能存在五重轴,这样的结构实际上只是对称性更低的 \(T_h\) 结构。
| 黄铁矿的晶面 | 黄铁矿-立方体形 | 黄铁矿-类五角十二面体形 |
|---|---|---|
 |  |  |
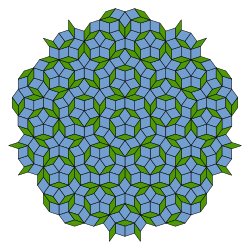
准晶体
事实上,通过某种方式真能结出来五角十二面体的晶体。某种Ho-Mg-Zn合金的晶体具有准晶(quasicrystal)的性质,其结构如下图所示,具有五重对称性但并不满足平移对称性,神奇的是居然能密铺整个空间。
| 准晶的微观结构 | 五角十二面体的准晶 |
|---|---|
 |  |
有趣的是,已知最早的准晶居然是“三位一体”核试验中的一块核爆玻璃样本。失重的魅力这一块,发现这个的也是神人了。
再比如说对于氧化亚铜 \(Cu_2O\) 的微晶,控制其结晶条件不同,可以获得含有多种晶面甚至高指数晶面的宏观晶体。
上述所探讨的都是单晶,即认为宏观晶体内只有一种连续的晶格结构。然而,由于结晶情况不同,有时候会由于产生了多种晶格结构而产生多晶。这样的产生的晶体内部并没有长程的平移对称性,可视为多种单晶形状的叠加。
1.1.4 液晶¶
液晶(Liquid Crystal)是一种介于液体和固体之间的一种状态,表示其中的分子像晶体一样有固定的趋向,但可以像液体一样流动。这样的分子通常需要很长且具有一定的刚性,如下图所示的分子MBBA:
通常情况下的液晶存在三种状态:
- 近晶相(Smectic phases):液晶仍然很大程度上趋向层状固体的排列方式,层间可以互相滑动。通常在较低的温度下产生。
- 向列相(Nematic phase):无晶体的整齐排列,但每个分子都近似呈平行趋向。通常在较高的温度下产生。
- 胆甾相/手性相(Chiral phases):由手性分子形成,存在螺旋扭曲。
| 近晶相 | 向列相 | 胆甾相 |
|---|---|---|
 |  |  |
1.2 晶体的宏观对称性¶
1.2.1 宏观对称元素¶
所谓“宏观对称性”,意思就是从宏观上可以观测到的对称性,包括旋转轴,反映面,反演中心三种。
什么叫“宏观可以观测”?
即最终会从宏观晶体上体现出来,对于旋转轴的信息,由于宏观晶体的晶面就是由微观晶体生长而来的,所以这个信息自然可以得到体现,如我们所看到的绝大部分晶体都是相对对称的图形。
与之相反的是,与平移相关的对称性不属于宏观对称性,因为宏观晶体是有限的,而平移是无限的。我们后面会说到这一类对称元素。
我们先从基本元素的记号出发。对于这三种对称元素一般记作(其中括号内的是讨论分子对称性的常用形式,括号外是讨论晶体对称性的常用形式):
- 旋转轴:\(1\ (C_1)\),\(2\ (C_2)\),\(3\ (C_3)\) ,\(4\ (C_4)\) ,\(6\ (C_6)\)
- 反映面: \(m\ (\sigma)\)
- 反演中心:\((i)\)
为什么只有这几种旋转轴?
这实际上被称为晶体学限制定理(crystallographic restriction theorem)。我们还是从平移对称性出发:
- 对于一个矢量连成的多边形而言,把所有矢量移到点中间构成一个相同对称性的图形,则对于6重对称以上的图形,平移后的多边形更小,如此重复会得到格点间距无限小的离谱结论。
- 对于五重对称而言,使其首尾相接形成五角星的五重对称图形,同样也会造成这一矛盾。
也可以通过三角学证明:
对于一个原子列,考虑向左和向右旋转 \(2\pi/n\) 的角。而由于平移对称性,其下面的点间距必须满足是原子间距的整数倍 \(r = ma\)。于是:
仅当 \(n=1,2,3,4,6\) 满足条件。
注意
很大程度上,分子的最高轴旋转轴和其形成的晶体的最高次旋转轴不一定一致。一个显而易见的例子是富勒烯 \(\ce{C60}\) ,你肯定不能指望一个晶体里有五次轴。
和分子对称性一样,如果我们将旋转操作和反演操作结合起来(即将(旋转 \(360/n^\circ\) + 反演一次)作为一步操作),我们就可以得到反轴。
- 反轴:\(\overline 1 \ (I_1, i)\), \(\overline 2 \ (I_2) \equiv m\),\(\overline 3 \ (I_3)\) ,\(\overline 4 \ (I_4)\) ,\(\overline 6 \ (I_6)\)
我们可以看到一重反轴(就是旋转一圈再反演)和反演中心完全一样,事实上在晶体里,我们一般更常用 \(\overline 1\) 记号代表反演中心。而对于二重反轴,其和反映面是相同的,但我们还是更常用反映面 \(m\) 的记号。
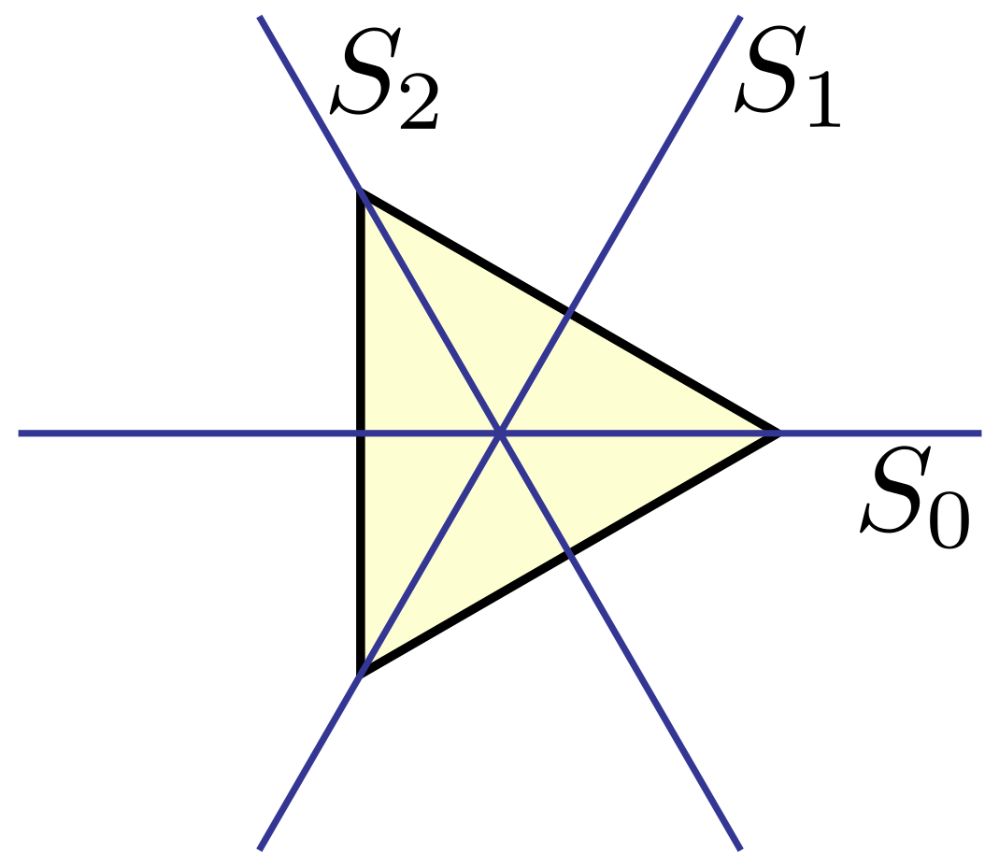
对于分子对称性,有一个类似的概念叫映轴(一般不在晶体对称性里提),即将(旋转 \(360/n^\circ\) + 沿对称轴反映一次)作为一步操作,事实上这和反轴是存在对应关系的:
| 反轴记号 | 对应的映轴记号 |
|---|---|
| \(\overline 1\) | \((S_2)\) |
| \(\overline 2 \equiv m\) | \((S_1)\) |
| \(\overline 3\) | \((S_6)\) |
| \(\overline 4\) | \((S_4)\) |
| \(\overline 6\) | \((S_3)\) |
1.2.2 晶系¶
我们前面提到,晶胞的选取需要整体是平行四边形/平行六面体。我们先从二维的平行四边形来考虑。
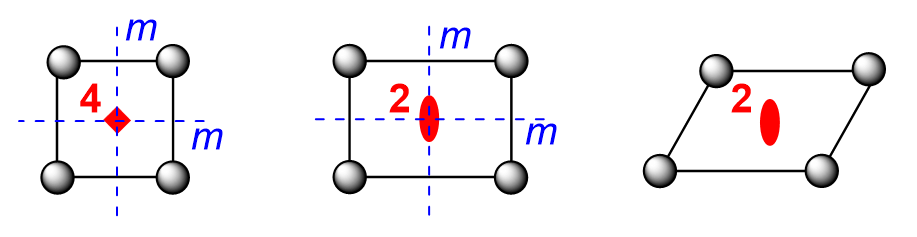
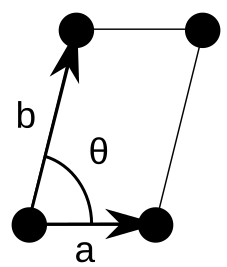
对于不同的平行四边形而言,其对称性是不同的。我们都知道,任何一个平行四边形都有二重旋转轴 \(2\) 。而当其夹角为直角时,其就会由平行四边形“进化”成矩形;再有邻边相等,就会“进化”成正方形。
如果科学的描述这个进化过程,实质上是对称性的提高:
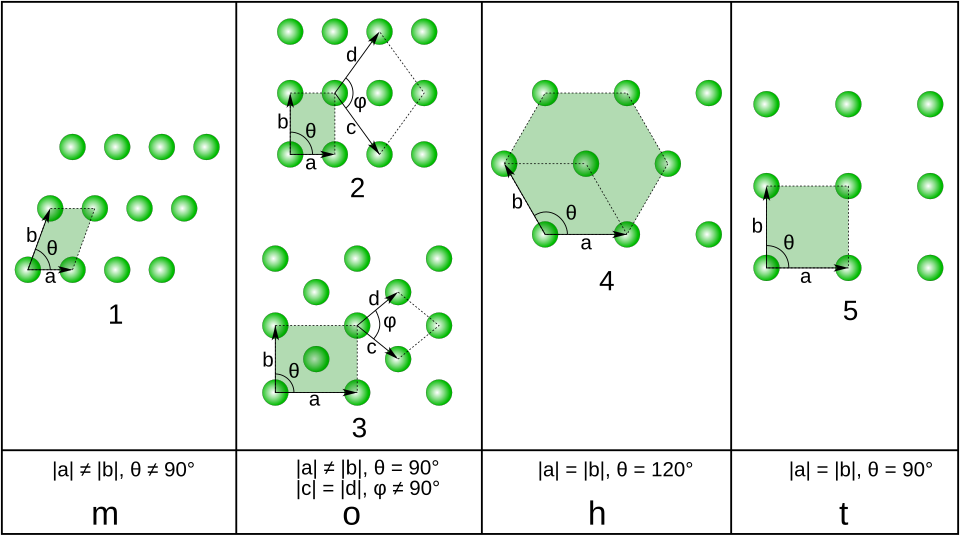
对于某类有相同对称性的晶格点阵,我们称之为属于一种晶系(Crystal System)。于是我们可以对二位点阵进行分类:
- 单斜晶系:“一般平行四边形晶胞(\(a\neq b, \alpha\neq 90^\circ\))”,仅有二重轴;
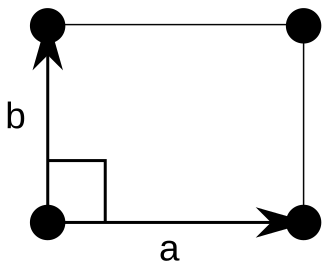
- 正交晶系:“矩形晶胞(\(a\neq b, \alpha = 90^\circ\))”,存在二重轴和两个垂直方向的镜面;
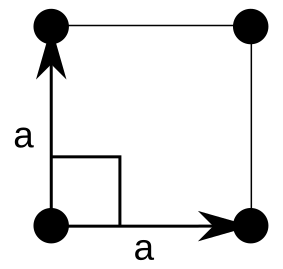
- 正方晶系:“正方形晶胞(\(a\neq b, \alpha = 90^\circ\))”,存在四重轴和两个垂直方向的镜面。
注意
我们说是“\(n\) 重轴”,指的是包括旋转轴,反轴,甚至后面要说的螺旋轴等所有对称轴,因为我们只管宏观对称性,而这些轴在宏观上并没有任何区别。
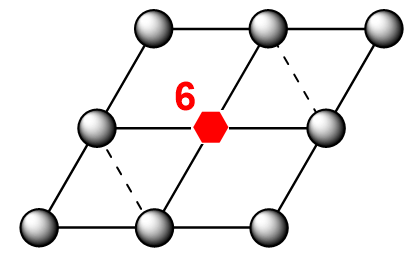
我们之前说过,晶体里还可能存在六重轴,但这里我们还没被讨论。事实上,六重轴需要对于整个点阵考虑,而不是对单个晶胞(因为平行四边形不可能有六重轴):
于是我们把这种情况单独提出来:
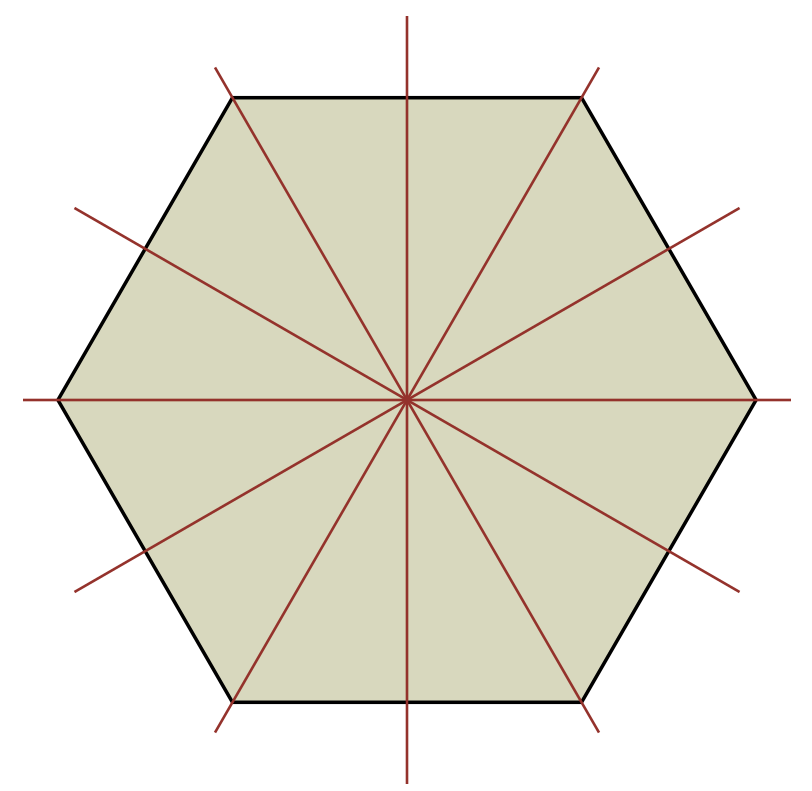
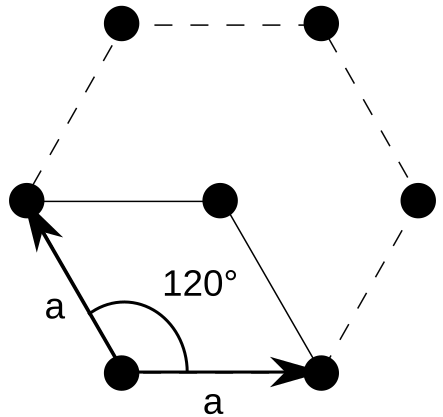
- 六方晶系:“(可画出)正六边形晶胞(\(a = b, \alpha = 120^\circ\))”,存在六重轴。
为什么没有三方晶系?
其原因是二维晶胞并不存在独立的三重轴。我们假设一个二维点阵分别在 \(A\) 和 \(B\) 存在二重旋转轴和三重旋转轴:
现在我们将点阵进行如下操作:
- 先绕 \(B\) 旋转 \(-120^\circ\);
- 再沿 \(\overrightarrow{BA}\) 方向平移;
- 再绕 \(A\) 旋转 \(-180^\circ\);
- 再沿 \(\overrightarrow{AB}\) 方向平移;
把这些操作加起来,你发现最终得到的点阵就是绕 \(B\) 点旋转 \(60^\circ\) 并平移得到的点阵,这意味着一定能找到某点 \(O\) 存在六重旋转轴。
我们假设 \(B\) 点在原点,而 \(A\) 对应复平面上的复数 \(a\) ,对于任意点 \(re^{i\theta}\):
- \(re^{i\theta} \rightarrow re^{i(\theta-2\pi/3)}\)
- \(re^{i(\theta-2\pi/3)} \rightarrow re^{i(\theta-2\pi/3)} + a\)
- \(re^{i(\theta-2\pi/3)} + a \rightarrow (re^{i(\theta-2\pi/3)} + a)e^{i\pi}\)
- \((re^{i(\theta-2\pi/3)} + a)e^{i\pi} \rightarrow (re^{i(\theta-2\pi/3)} + a)e^{i\pi} -a = re^{i(\theta+\pi/6)} -2a\)
于是六重旋转中心位于 \(\overrightarrow{BO} = 2\overrightarrow{BA}\) 处。
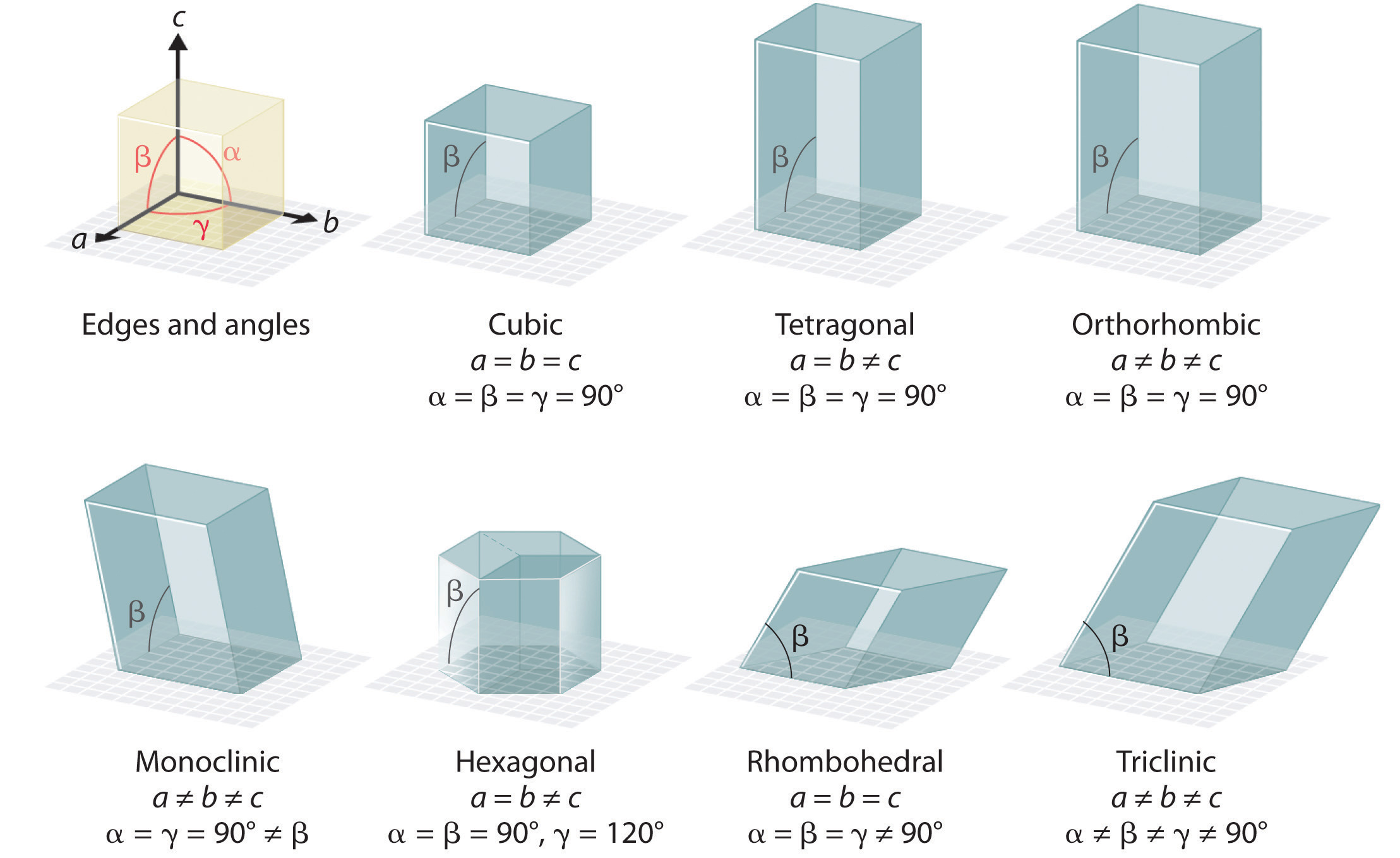
接下来我们从二维拓展到三维。对于最低对称性平行六面体,其最多存在一重轴(相当于最多只能存在一个对称中心)。我们依次往上叠加对称性:
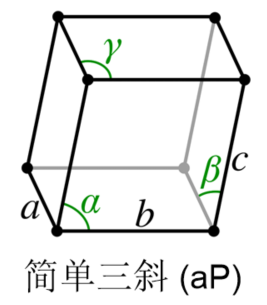
- 三斜晶系(Triclinic):“一般平行六面体晶胞(\(a\neq b \neq c, \alpha \neq \beta \neq \gamma \neq 90^\circ\))”,仅有一重轴;
- 单斜晶系(Monoclinic):“平行四边形直柱(\(a\neq b \neq c, \alpha = \gamma = 90^\circ,\beta \neq 90^\circ\))”,有一个平行于 \(b\) 轴的二重轴;
- 正交晶系(Orthorhombic):“长方体(\(a\neq b \neq c, \alpha = \beta = \gamma = 90^\circ\))”,有三个相互垂直的二重轴;
- 四方晶系(Tetragonal):“底面是正方形的长方体(\(a = b \neq c, \alpha = \beta = \gamma = 90^\circ\))”,有一个平行于c轴的四重轴。
- 立方晶系(Cubic):“立方体(\(a = b = c, \alpha = \beta = \gamma = 90^\circ\))”,有四个体对角线上的三重旋转轴。
特别注意
对于立方晶系,特别注意这里的三重轴必须是严格的三重旋转轴(三重反轴包括在内),这一特性也使“是否有四个方向的三重旋转轴”称为判断是否立方晶系的标准手段,甚至有的立方晶系晶体都可以不包含四重旋转轴(如 \(\ce{NaClO3}\),这是一个手性晶体)。
同样的,我们考虑关于三次轴和六次轴的特殊情况:
- 三方晶系(Trigonal,有的书也叫菱方晶系Rhombohedral):“(可画成)正六棱柱晶胞(\(a = b \neq c, \alpha = \beta = 90^\circ, \gamma = 120^\circ\)) 或 菱方晶胞(\(a = b = c, \alpha = \beta = \gamma \neq 90^\circ\))”,有一个独立的三重轴。
- 六方晶系(Hexagonal):“(可画成)正六棱柱晶胞(\(a = b \neq c, \alpha = \beta = 90^\circ, \gamma = 120^\circ\))”,有一个六重轴。
结合我们在二维晶系的结论,我们可以知道:如果一个三方晶系存在平行于c轴的二重轴(平行于c轴的二重旋转轴或是垂直于c轴的镜面),那么就会升级成六方晶系。
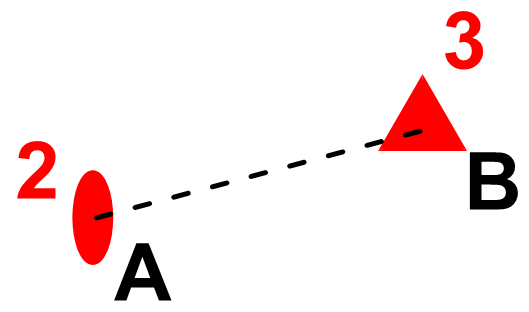
特征对称元素
特征对称元素就是说能判定这个晶体是某个晶系的最佳判据。例如,对于一个四方晶系的晶体,特征对称元素就是其四重旋转轴或四重反轴或四重螺旋轴;对于一个立方晶系的晶体,特征元素就是四个三次旋转轴。
需要注意两个特殊的情况:
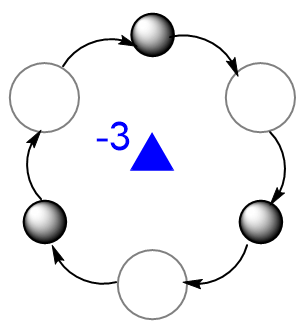
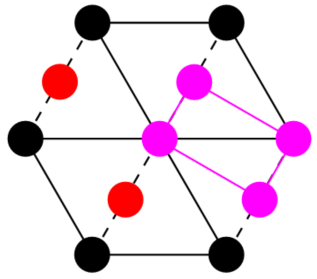
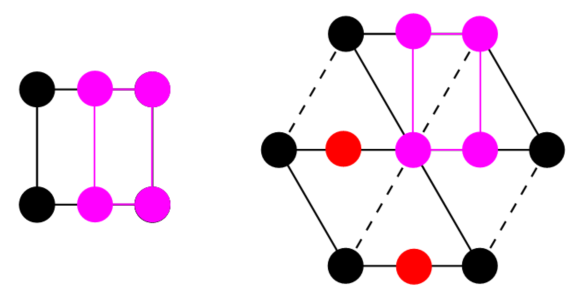
- 同时存在 \(\bar 3\) 和 \(3\) :注意三重反轴的作用,其中浅色大球代表位于平面下方与黑球对称的球:
于是对于三重反轴,实际上就是三重旋转轴+对称中心,其包含的内容比三重旋转轴更多,因此我们认为特征对称元素是 \(\bar 3\) 。 这也意味着立方晶系同样允许三重反轴代替三重旋转轴(因为前者更高级)。
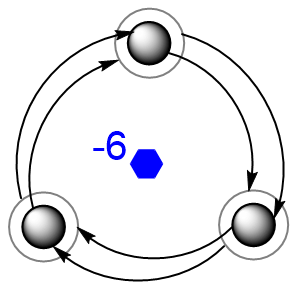
- 同时存在 \(\bar 6\) 和 \(6\) :同样注意六重反轴的作用:
六重反轴是三重旋转轴+镜面,而对比来说六重轴包含的信息肯定更多,因此我们认为特征对称元素是 \(6\) 。
1.2.3 晶体学点阵(晶类)¶
如果我们用晶系描述晶体对称性,实际上是不完全的,因为我们只描述的特征对称元素。要想描述所有对称元素,我们需要知道这些信息:
- 对称元素是什么?
- 对称元素在哪里?
对第一个问题,我们前面已经说过可以用符号来表示;而第二个问题,就需要知道对于每个晶系而言,对称元素可能出现的位置在哪里。
以立方晶系而言,其对称元素可能出现在{100},{110},{111}三个方向上,对应的矢量分别是\(\vec a, \vec a +\vec b, \vec a +\vec b + \vec c\)。而在这三个方向上,可能出现的最高次轴的轴次分别是四重轴,二重轴和三重轴,我们按从高到低排序得到:
这里三个框的意思是“有三个待定位置等待填入”,而这三个位置分别在 \(\vec a, \vec a +\vec b + \vec c, \vec a +\vec b\) 这三个矢量上。
对于其他晶系,我们也做如此排序:
- 四方晶系:\(\boxed{\vec c}\ \boxed{\vec a}\ \boxed{\vec a + \vec b}\)
-
正交晶系:\(\boxed{\vec a}\ \boxed{\vec b}\ \boxed{\vec c}\)
-
六方晶系:\(\boxed{\vec c}\ \boxed{\vec a}\ \boxed{2\vec a + \vec b}\)
-
三方晶系:\(\boxed{\vec c}\ \boxed{\vec a}\)
-
单斜晶系:\(\boxed{\vec b}\)
-
三斜晶系:\(\boxed{\vec a}\)
六方晶系的有点奇怪,实际上这就是对应正六边形的两种对称轴:
而对应的三方晶系来说,就不存在 \(2\vec a + \vec b\) 这一种对称模式:
这样定向之后有什么用呢?我们在每个框里都填了一种对称元素对应的方向,接下来只需要把对应的对称元素填进去就好了。
我们以四方晶系举例,如果在 \(c\) 轴的位置存在四重旋转轴(或之后要说的四重螺旋轴),第一个框内就填入 \(4\) ;如果是四重反轴,第一个框内就填入 \(\bar 4\);如果同时存在四重旋转轴和镜面,第一个框内就一般填入 \(4/m\) 。其他框内也是同理,如果这个位置没有对称元素,就留空。
如此这样,我们就可以把晶体的所有对称元素全部表示出来,以这样的表达式归类晶体被称为晶类(Crystal Class)或晶体学点群(Crystallography Point Group),这种记号被称为 Hermann-Mauguin 记号(H-M Symbol)。
判断晶类
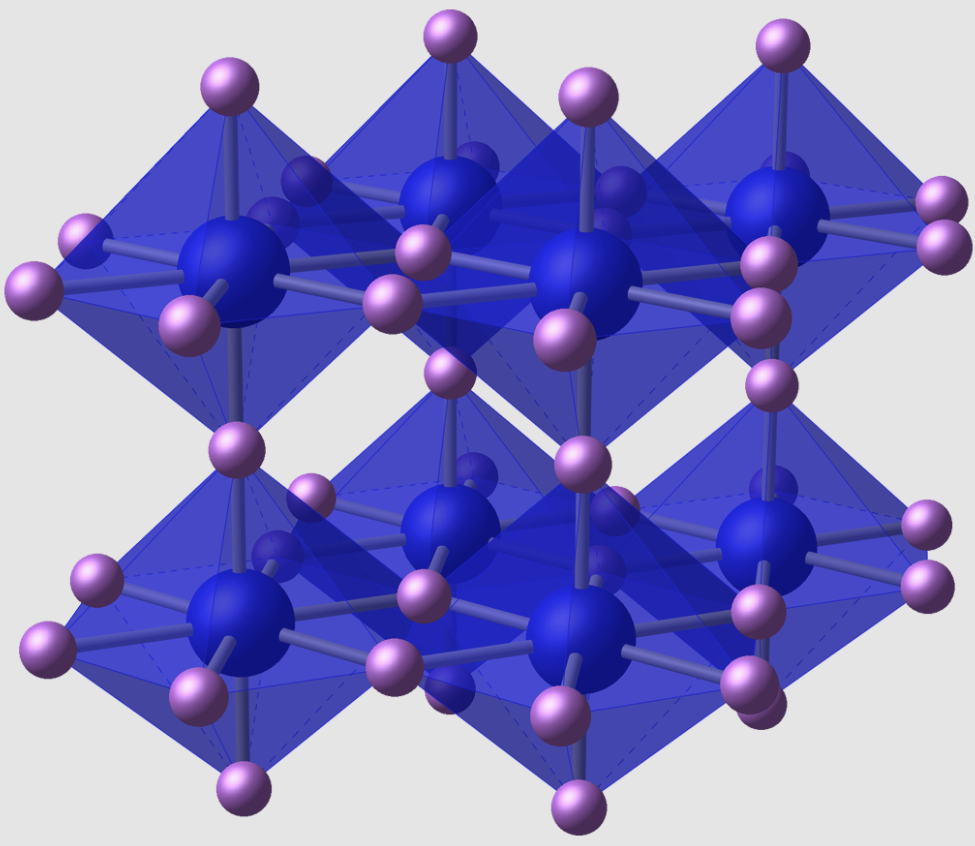
给出如图所示的氮化锂晶体的晶类。
答案
很明显这是一个六方晶系且存在一个 \(C_6\) 轴,在其垂直方向存在镜面,因此 \(\vec c\) 方向的对称元素是 \(6/m\) 。
之后,在其余的两个方向上都存在 \(2/m\) 对称元素。为了简便,对于次级的二重对称轴和镜面同时存在,一般只写镜面。因此后面两个对称元素都写作 \(m\) 。
于是就可以得到其晶类:\(6/mmm\) 。
很明显,晶体学点群也是点群,所以另一种表示方法是通过分子点群的表示法表示。我们前面说过,晶体中的轴次只包含 \(n = 1,2,3,4,6\),我们依次将他们设为主轴:
| \(n\) | \(1\) | \(2\) | \(3\) | \(4\) | \(6\) |
|---|---|---|---|---|---|
| \(C_n\) | \(C_1\) | \(C_2\) | \(C_3\) | \(C_4\) | \(C_6\) |
| \(C_{nv}\) | \(C_{1v}=C_{1h}\) | \(C_{2v}\) | \(C_{3v}\) | \(C_{4v}\) | \(C_{6v}\) |
| \(C_{nh}\) | \(C_{1h}\) | \(C_{2h}\) | \(C_{3h}\) | \(C_{4h}\) | \(C_{6h}\) |
| \(D_n\) | \(D_1=C_2\) | \(D_2\) | \(D_3\) | \(D_4\) | \(D_6\) |
| \(D_{nh}\) | \(D_{1h}=C_{2v}\) | \(D_{2h}\) | \(D_{3h}\) | \(D_{4h}\) | \(D_{6h}\) |
| \(D_{nd}\) | \(D_{1d}=C_{2h}\) | \(D_{2d}\) | \(D_{3d}\) | \(D_{4d}\) | \(D_{6d}\) |
| \(S_{2n}\) | \(S_2\) = \(C_i\) | \(S_4\) | \(S_6\) = \(D_{3h}\) | \(S_8\) | \(S_{12}\) |
注意表格右下角的几个点群,它们都有着过高的反轴轴次(\(I_8\) 或 \(I_{12}\)),因此在晶体学中不存在,加以排除。剩下的除去相同点群还剩下27个点群。
当然,不要忘了还有多面体群:
| 四面体群 | \(T, T_d, T_h\) |
|---|---|
| 立方体群 | \(O, O_h\) |
注意对于十二面体群,由于存在晶体学中不存在的五重轴,因此被排除。
这五个点群加上之前讨论的一共32个点群,构成了晶体学中可能存在的所有晶类。
| 晶系 | 基本情形 | 含反轴 | 含主镜面 | 含2个次轴 | 含2个次镜面 | 含次轴和次镜面 | 含3个镜面 |
|---|---|---|---|---|---|---|---|
| 立方晶系 | \(23\)(\(T\)) | \(m\overline{3}\)(\(T_h\)) | \(\overline{4}32\)(\(O\)) | \(\overline{4}3m\)(\(T_d\)) | \(m\overline{3}m\)(\(O_h\)) | ||
| 六方晶系 | \(6\)(\(C_6\)) | \(\overline{6}\)(\(C_{3h}\)) | \(6/m\)(\(C_{6h}\)) | \(622\)(\(D_6\)) | \(6mm\)(\(C_{6v}\)) | \(\overline{6}m2\)(\(D_{3h}\)) | \(6/mmm\)(\(D_{6h}\)) |
| 三方晶系 | \(3\)(\(C_3\)) | \(\overline{3}\)(\(S_6\)) | \(32\)(\(D_3\)) | \(3m\)(\(C_{3v}\)) | \(\overline{3}m\)(\(D_{3d}\)) | ||
| 四方晶系 | \(4\)(\(C_4\)) | \(\overline{4}\)(\(S_4\)) | \(4/m\)(\(C_{4h}\)) | \(422\)(\(D_4\)) | \(4mm\)(\(C_{4v}\)) | \(\overline{4}2m\)(\(D_{2d}\)) | \(4/mmm\)(\(D_{4h}\)) |
| 正交晶系 | \(222\)(\(D_2\)) | \(mm2\)(\(C_{2v}\)) | \(mmm\)(\(D_{2h}\)) | ||||
| 单斜晶系 | \(2\)(\(C_2\)) | \(2/m\)(\(C_{2h}\)) | \(m\)(\(C_s\)) | ||||
| 三斜晶系 | \(1\)(\(C_1\)) | \(\overline{1}\)(\(C_i\)) |
你并不需要精确的记忆每一种晶类,只需掌握其逻辑判断方法即可。读者不妨选择几种记号,试着思考一下对称元素分布的位置。
1.3 微观对称元素¶
1.3.1 二维点阵形式¶
前面说过,宏观对称元素就是不包含平移的对称操作,而相反,微观对称元素就是包含单一方向平移的对称操作。
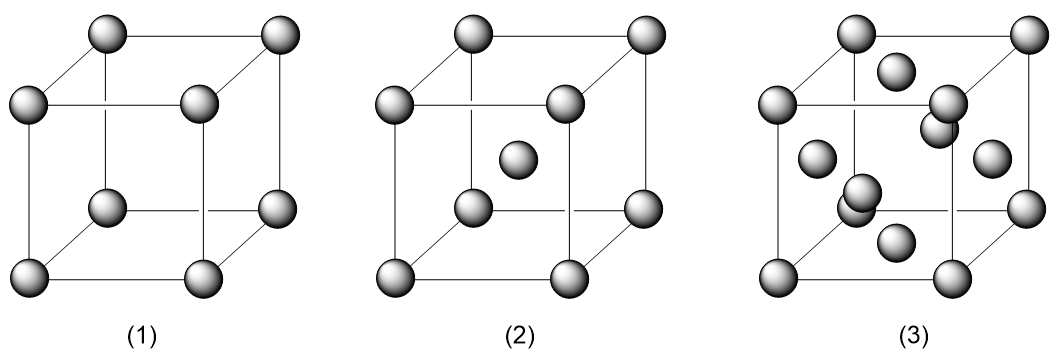
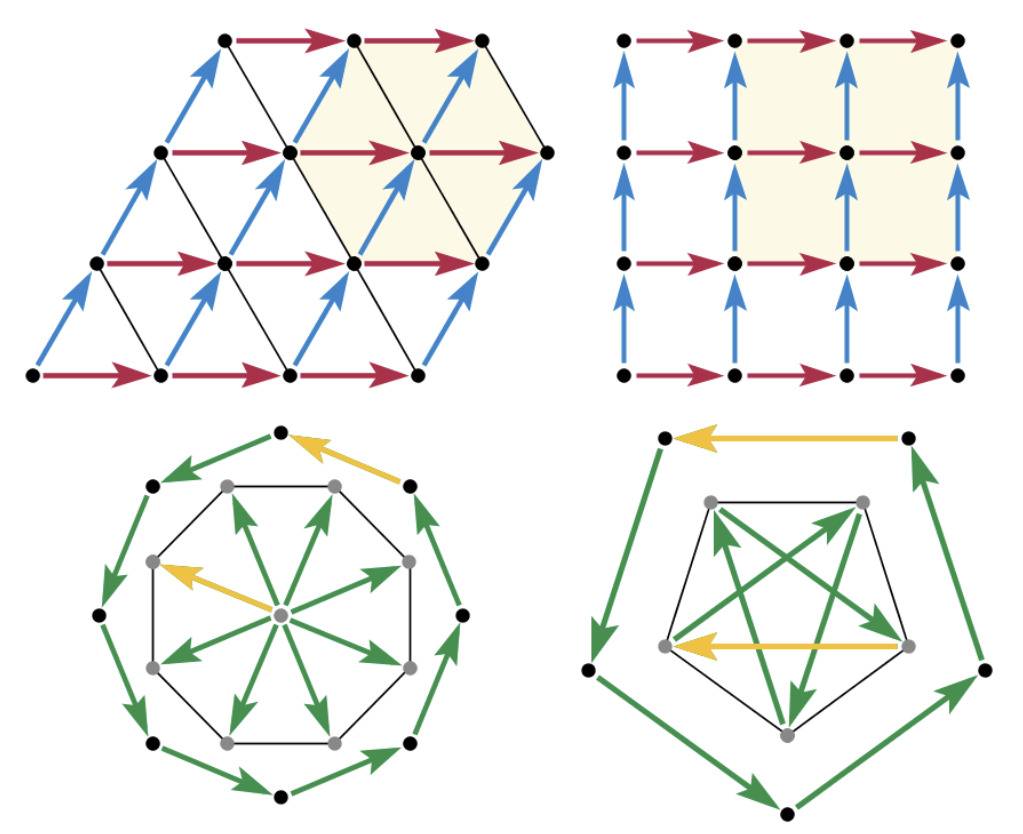
我们先从“平移”这个操作开始说起。我们知道,“晶胞”本身就是可以通过平移重复的单元,于是很自然的想到,对于任意一个晶体而言,只需考虑沿晶胞轴方向的平移就一定能重合。以二维晶胞作为例子:
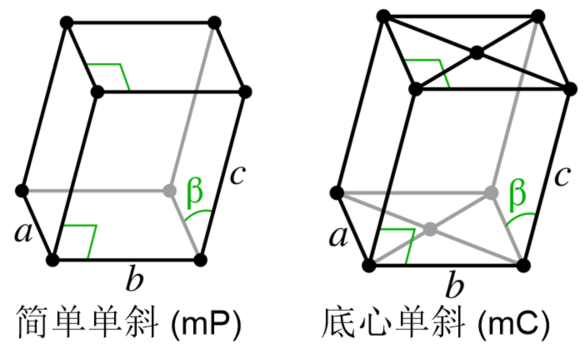
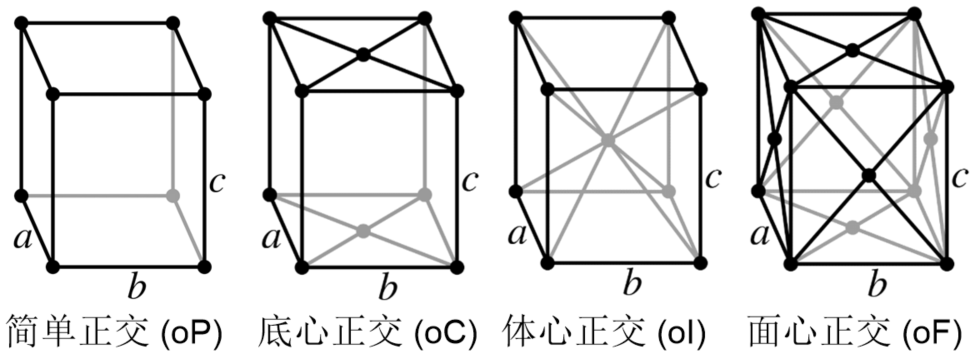
| 简单单斜 | 简单正交 | 简单正方 | 简单六方 |
|---|---|---|---|
 |  |  |  |
我们考虑完全了吗?其实并没有,因为我们只考虑点阵点在晶胞顶点的情况。如果在晶胞内部还存在点阵点呢?
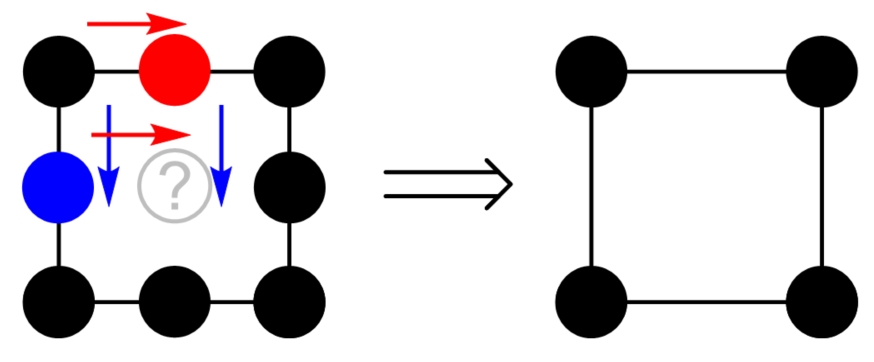
从平移对称性我们知道,如果内部存在点阵点,那么其只能位于中心或棱心处,因为这样才能使相同距离平移时仍有对应的点可以重合(也就是先平移原向量一半的向量到达“心”点,之后再次平移到原向量)。
当然也有可能是在整数分之一的位置加多个棱心,但由于平移对称性可知这样加点和加在棱心是等同的。
回到这四种晶胞本身,我们考虑在中心加入点阵点会带来什么改变:
| 带心单斜 | 带心正交 | 带心正方 | 带心六方 |
|---|---|---|---|
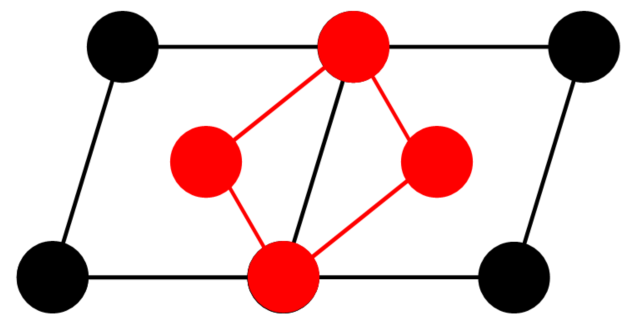 | 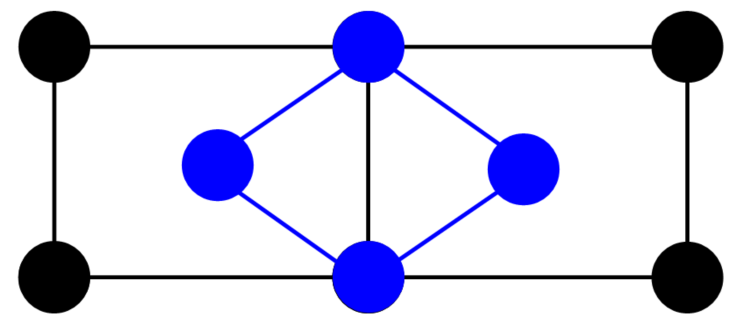 | 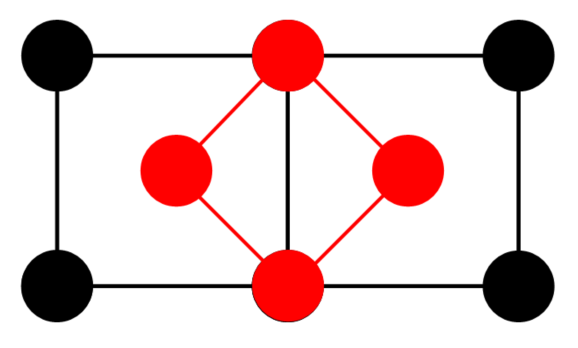 |  |
你可以注意到:加心不是没有代价的。对于一个加心的晶胞而言,我们总能找到一个更小的正当晶胞。回顾之前我们说过的“晶胞三原则”:
- 完全反映点阵的对称性;
- 包含尽可能多的直角;
- 体积尽量小(但不一定是最小)。
注意到“体积尽量小”这一条的重要性是最低的,可他毕竟也是一项啊!因此,在一般的情况下,晶胞都会“坍缩”成更小的同等的晶胞,除非它波坏了前两个要求:
- 加心破坏了原晶胞的对称性;
- 或着 加心画出的更小晶胞直角数比原晶胞更少。
对于第一条,首当其冲的就是六方晶胞。我们知道六方晶胞满足 \(C_6\) 对称性,而加心会把这个旋转轴降级成 \(C_2\) 。当然对称面是还在的,因此我们大概知道带心的简单六方会退化成简单正交。我们也可以通过画图证明这一点:
而对于第二条,回顾这些带心晶胞,仅有带心正交一种画出的小晶胞直角数更少,因此“带心正交”这种点阵形式就被保留了下来。而对于带心单斜和和带心正方而言就没有这种福利了:它们统统都会退化成简单点阵。
汇总一下:(向右箭头表示“退化成同等级点阵形式”,向下箭头表示“退化成低等级点阵形式”,)
| 单斜 | 正交 | 正方 | 六方 | |
|---|---|---|---|---|
| 简单 | 简单单斜 | 简单正交 | 简单正方 | 简单六方 |
| 带心 | 带心正交 |
在晶体学中,我们也把这种可以取更小正当晶胞的点阵称为复点阵,就相当于是多个正当晶胞的叠加。
对于棱心而言,很容易就得到单斜和正交都能画出直角数不变的更小晶胞。而对于正方和六方而言会退化成对称性更低的点阵形式:
疑惑
为什么不存在两个棱都加心的点阵呢?这是因为这根本不是一个点阵,因为连续沿a方向和b方向移动半个单位长度的地方并没有原子。事实上,这是一个简单点阵,其新点阵点包括原来的3个点阵点。
在三维情况下也是同理,不存在“所有棱都加心”的点阵。
1.3.2 三维点阵形式(前篇)¶
二维的事情说完了,我们来聊聊三维的情况。三维总共要考虑 三斜a,单斜m,正交o,四方t,立方c,六方h,三方r 这么多晶系,而可能加的心也增加到了 面心F,体心I,A心A,B心B,C心C 这五种(A、B、C心分别指在α,β,γ轴对应的面上加面心)。
附加的字母是表示晶系或者加心的代号字母,比如面心立方可以简写成cF,体心四方可以简写成tI。
对于三斜来说最简单了:因为它根本没有对称性,所以无论怎么加心都能找到一个更小的正当晶胞。它们都是简单三斜点阵。
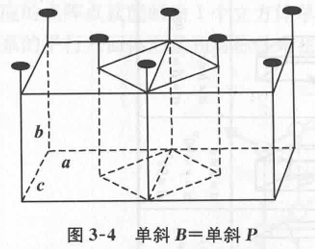
对于单斜点阵,记住他的晶胞结构相当于底面是平行四边形的直四棱柱。我们可以把它拆解成两个投影:其中沿b轴的投影是简单单斜,沿c轴的投影式简单正交。
我们前面又说过,只有正交点阵才能加心产生新点阵,因此B心单斜会退化成简单单斜。而C心单斜是一个新点阵,同理A心单斜也是一个新点阵,但由于一般情况下a轴和c轴可以调换(就是换个记号的事情),所以我们都把他们统称成底心单斜点阵(mC)。
注意
这个“底心”的说法有点误导人,因为理论上我们把这个晶胞视作直四棱柱的时候,它的“底面”应该是B面。所以这里的加心理论上加的是“侧心”,只不过约定俗成了。
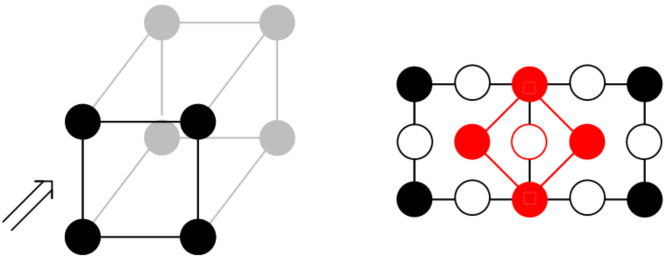
再来看体心。对于二维来说我们没有考虑这种情况,是因为所有的点都是等同的;但是三维里我们需要考虑不同高度的点在投影图上是不同的。对此我们通过画投影图的方式(其中空心球代表在 b = 1/2 处有点阵点,实心球表示在 b = 0 处有点阵点)可以看出它们都是底心单斜的复点阵。
于是我们知道:单斜点阵有 简单单斜 (mP) 和 底心单斜 (mC) 两种。
对于正交点阵而言,因为三个方向的投影图都为二维正交点阵,因此任何方式的带心都无法画出更小的正当晶胞。
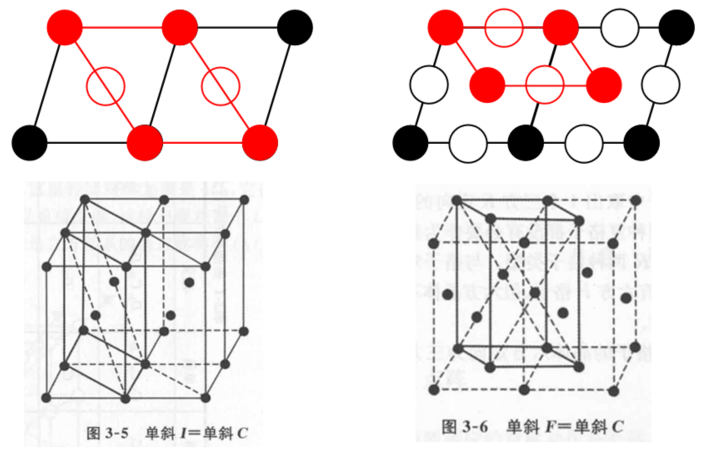
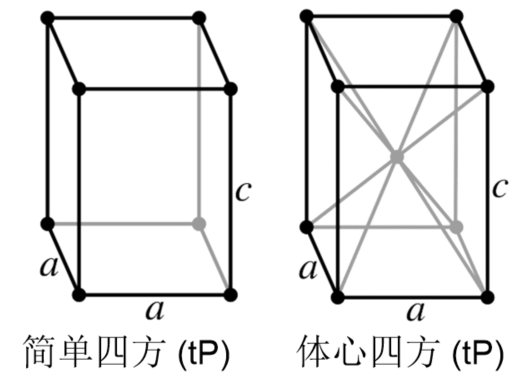
再来看四方。对于四方点阵,在A面或者B面加心都会导致对称性的破缺,把点阵降级成底心正交。
观察沿底面的投影图可以知道这是一个二维正方点阵,因此加底心可以取更小的晶胞。而面心四方点阵可以画出更小的体心四方点阵,体心四方就画不出更小的了:
因此我们知道:四方点阵总共有2个点阵形式: